Skip to content

5주차 BFS, DFS

Jump to bottom
Wonjun You edited this page Feb 5, 2023 · 3 revisions

완전탐색(Exhaustive Search)

💡 가능한 모든 경우의 수를 탐색하여 정답을 찾는 방법을 의미함.

완전탐색의 대표적인 유형들은 다음과 같다.

  • Brute Force(브루트 포스 : 무식하게 푼다)
  • BFS(너비 우선 탐색), DFS(깊이 우선 탐색)
  • 순열/조합
  • 비트마스킹

완전탐색의 특징 (ex 서랍에서 물건 찾기)

  • 자원만 충족된다면 100%의 정답률을 보장.
  • 모든 경우의 수를 다 탐색하기 때문에 가장 시간이 느리다.

선형 구조의 완전탐색 vs 비선형 구조의 완전탐색

선형 자료구조

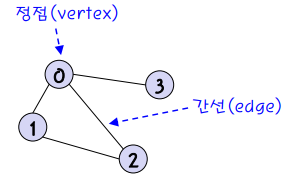
  • 하나의 노드 뒤에 하나의 노드가 존재하는 자료구조를 말한다.
  • 배열, 리스트, 스택, 큐가 포함된다.
  • 브루트 포스(brute force) 기법을 이용한 완전탐색을 한다.

image

비선형 자료구조

  • 하나의 노드 뒤에 여러 개의 노드가 존재하는 자료구조를 의미한다.
  • 그래프, 트리 등이 이에 해당된다.

image

→ 탐색 시에 순서가 정해져 있지 않기 때문에, 큐나 스택 등의 특정 자료구조를 사용하여 순서를 정해야 한다.


그래프를 표현하는 방법

인접 행렬과 인접 리스트

  • 인접 행렬

image

  • N*N 크기의 2차원 배열을 생성해서 연결 상태를 나타낸다.

  • 인접 리스트

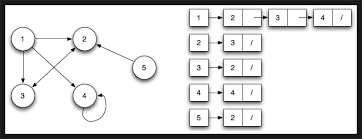
image

  • N개의 리스트를 생성해서 연결 상태를 나타내는 방법.

BFS와 DFS : 가중치가 없는 그래프에서 사용하는 탐색 기법

image

BFS(Breadth First Search)

  • 너비 우선 탐색이라는 뜻으로, 시작 정점에서 가까운 점을 우선 방문하고, 멀리 있는 점을 나중에 방문하는 기법이다.
  • 자료구조 중 큐를 사용한다.
  • 시간 복잡도는 O(|V| + |E|)이다.

DFS(Depth First Search)

  • 깊이 우선 탐색이라고 하며, 더 이상 깊이 탐색할 수 없을 때 까지 탐색 후에 다시 빠져나오는 과정을 반복하며 탐색하는 기법이다.
  • 주로 스택 이나 재귀 를 통해 구현한다.
  • 시간 복잡도는 O(|V| + |E|)이다.

예제 문제 풀이 1 : 백준 1260 DFS와 BFS

문제 링크


정답 코드 
from collections import deque
import sys

input = sys.stdin.readline

def bfs(v):
    q = deque()
    q.append(v)
    visited[v] = 1

    while q:
        v = q.popleft()
        result_for_bfs.append(v)

        for i in range(1, n+1):
            if graph[v][i] == 1 and visited[i] == 0:
                q.append(i)
                visited[i] = 1

def dfs(v):
    result_for_dfs.append(v)
    visited[v] = 1
    
    for i in range(1, n+1):
        if graph[v][i] == 1 and visited[i] == 0:
            dfs(i)

n, m, v = map(int, input().rstrip('\n').split())

graph = [[0] * (n+1) for _ in range(n+1)]
visited = [0] * (n+1)

result_for_bfs = []
result_for_dfs = []

for _ in range(m):
    v1, v2 = map(int, input().rstrip('\n').split())

    graph[v1][v2] = graph[v2][v1] = 1

dfs(v)
print(*result_for_dfs)

visited = [0] * (n+1)

bfs(v)
print(*result_for_bfs)

코테에서의 BFS와 DFS는 주로 2차원 배열에서 이루어진다.

💡 2차원 배열은 가중치가 없는 무향 그래프로써 활용될 수 있기 때문이다.

[유향 그래프 VS 무향 그래프]

image


[가중치가 없는 그래프 vs 가중치가 있는 그래프]

image


[2차원 배열에서의 BFS, DFS]

image

과정은 다음과 같다.

  1. (0, 0)을 시작점으로 놓고, 해당 좌표값을 큐에 넣는다.
  2. 큐의 가장 앞에 있는 값을 꺼내어 해당 좌표로 이동(탐색)한다.
  3. (0, 0)에서 다음 차례에 이동 가능한 좌표는 (1, 0), (0, 1)이므로, 해당 좌표를 큐에 넣는다.
  4. 2와 3을 반복하여 탐색한다.

dfs도 동일하나, stack 을 이용하기 때문에 LIFO 성질에 의해 가장 최근에 방문한 칸에서 추가 탐색이 이루어진다는 점에서 차이가 있다.

예제 문제 풀이 2 : 백준 2667 단지번호붙이기

문제 링크


정답 코드 
import sys

input = sys.stdin.readline

def dfs(x, y):
    global count
    visited[x][y] = 1

    for i in range(4):
        nx = x + dx[i]
        ny = y + dy[i]

        if (0<=nx<n and 0<=ny<n):
            if graph[nx][ny] == 1 and visited[nx][ny] == 0:
                count += 1
                dfs(nx, ny)

    return count

n = int(input().rstrip('\n'))

graph = []
visited = [[0] * n for _ in range(n)]

dx = [-1, 1, 0, 0]
dy = [0, 0, 1, -1]

result = []

for _ in range(n):
    graph.append(list(map(int, input().rstrip('\n'))))

for i in range(n):
    for j in range(n):
        if graph[i][j] == 1 and visited[i][j] == 0:
            count = 1
            result.append(dfs(i, j))

result.sort()

print(*result)

BFS는 거리를 측정할 수 있으며, 따라서 최단거리 알고리즘에 이용된다.

image

최단거리 알고리즘의 종류

  • 다익스트라 알고리즘
  • 벨만-포드 알고리즘
  • 플로이드-워셜 알고리즘 등등..

근데 왜 BFS?

→ BFS는 가중치가 없거나(unweighted), 가중치가 일정한 경우에도 사용할 수 있다.
→ 가중치가 0, 1로 이루어진 경우에 사용 가능(0-1 BFS)

그렇다면 DFS는 안 될까?

→ 결론부터 말하면 안 된다.
→ DFS가 한 단계 더 진행되었다고 하더라도, 반드시 거리가 1 증가한다는 것을 보장하지 않기 때문이다.


함께 공부할 문제 리스트

난이도 문제명 분류
[1260] DFS와 BFS 그래프 이론 그래프 탐색 너비 우선 탐색 깊이 우선 탐색
[2667] 단지번호붙이기 그래프 이론 그래프 탐색 너비 우선 탐색 깊이 우선 탐색
[1012] 유기농 배추 그래프 이론 그래프 탐색 너비 우선 탐색 깊이 우선 탐색
[2178] 미로 탐색 그래프 이론 그래프 탐색 너비 우선 탐색
[1697] 숨바꼭질 그래프 이론 그래프 탐색 너비 우선 탐색
[7576] 토마토 그래프 이론 그래프 탐색 너비 우선 탐색
[7569] 토마토 그래프 이론 그래프 탐색 너비 우선 탐색
[16234] 인구 이동 구현 그래프 이론 그래프 탐색 너비 우선 탐색 시뮬레이션
[16928] 뱀과 사다리 게임 그래프 이론 그래프 탐색 너비 우선 탐색
[2573] 빙산 구현 그래프 이론 그래프 탐색 너비 우선 탐색 깊이 우선 탐색
Clone this wiki locally