A5: Sierpenski

Refer back to A1 for information on running the development server, and with running tests locally.

The Sierpenski Triangle is a popular mathematical fractal which recursively subdivides an equilateral triangle. As with a fractal, it is a generated pattern than can be infinitely subdivided and zoomed in on.

The way a Sierpenski Triangle is created is quite simple, though the implementation a bit more challenging. In essence, these are the steps:

1. Start with an equilateral triangle
2. Subdivide it into four equal parts and remove the center triangle
3. Repeat step 2 with each of the remaining triangles ad infinitium

In this assignment, you will write the code to recreate this famous triangle through recursion and the HTML <canvas>. We’ll also brush up on the math required to generate an equilateral triangle.

Canvas

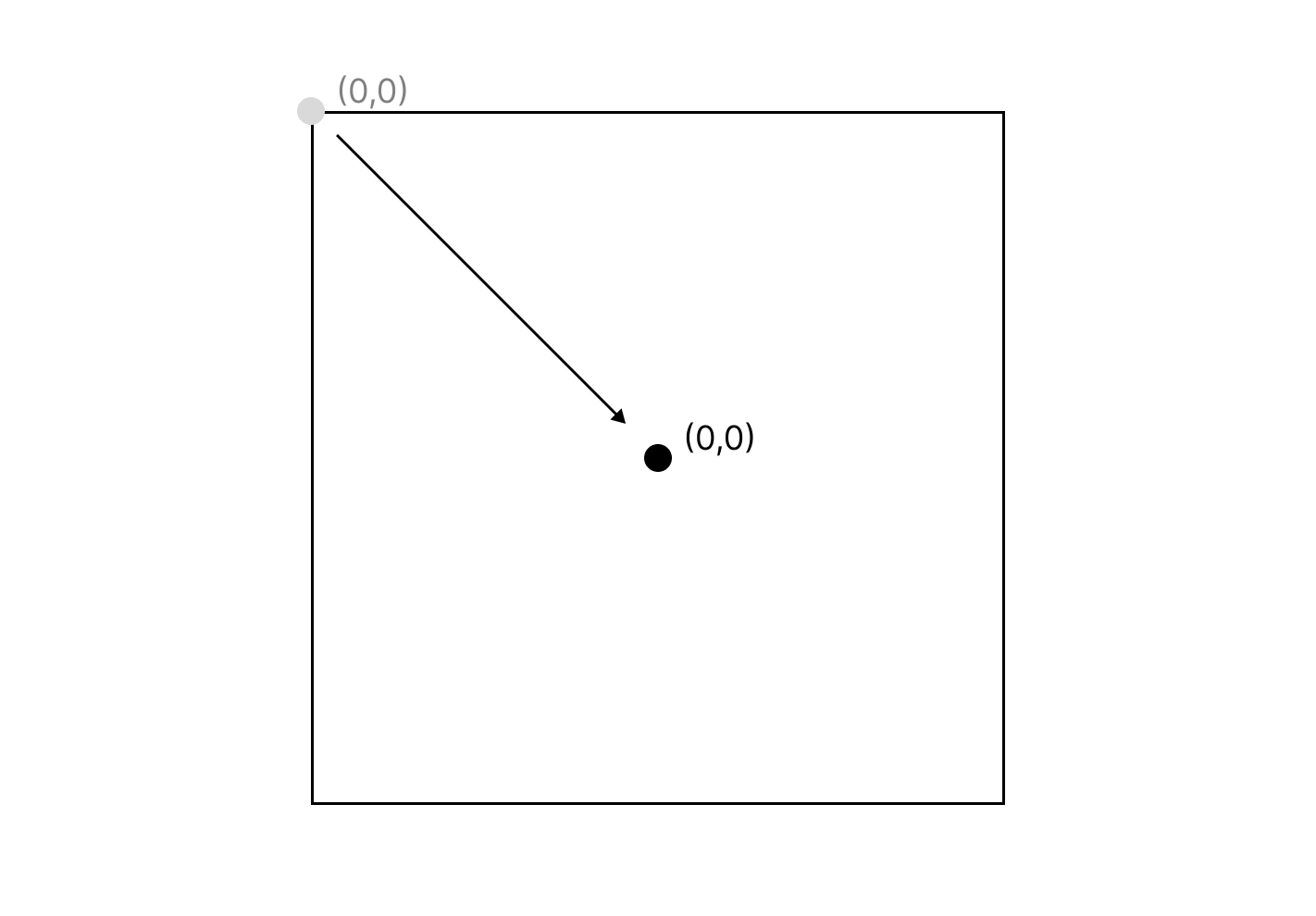
The HTML canvas is a powerful tool, letting you create both 2D and 3D objects within it. For our case, we will be sticking with 2D rendering. Normally, the origin of the canvas begins at the top left corner. However, since we are dealing with cartesian coordinates, we will begin my resetting the origin to the center of the canvas by calling translate() in the constructor:

Note that even if we do this, the y-axis still increases going downwards.

To draw in a canvas, you must access its context. This exists as part of the canvas which lets you draw shapes. You’ve actually used it in the N-Body assignment, though it was abstracted for you. This time, you’ll be accessing it directly. You can access the context of a canvas by calling let ctx = canvas.getContext('2d');. From here, you can do many different operations including:

ctx.fillRect(0, 100, 50, 50) // Draws a square with width and height 50 where its top left corner is at (0, 100).
ctx.fillRect(25, 30, 100, 10) // Draws a rectangle with width 100 and height 10 where its top left corner is at (25, 30).

// Draw a path from (20, 20) to (50, 30) to (50, 50)
ctx.beginPath(); // Tells canvas to begin drawing the path
ctx.moveTo(20, 20); // Moves the drawing pencil to (20, 20)
ctx.lineTo(50, 30); // Draws a line from (20, 20) to (50, 30)
ctx.lineTo(50, 50); // Draws a line from (50, 30) to (50, 50)
ctx.closePath(); // Tells canvas to finish drawing the path

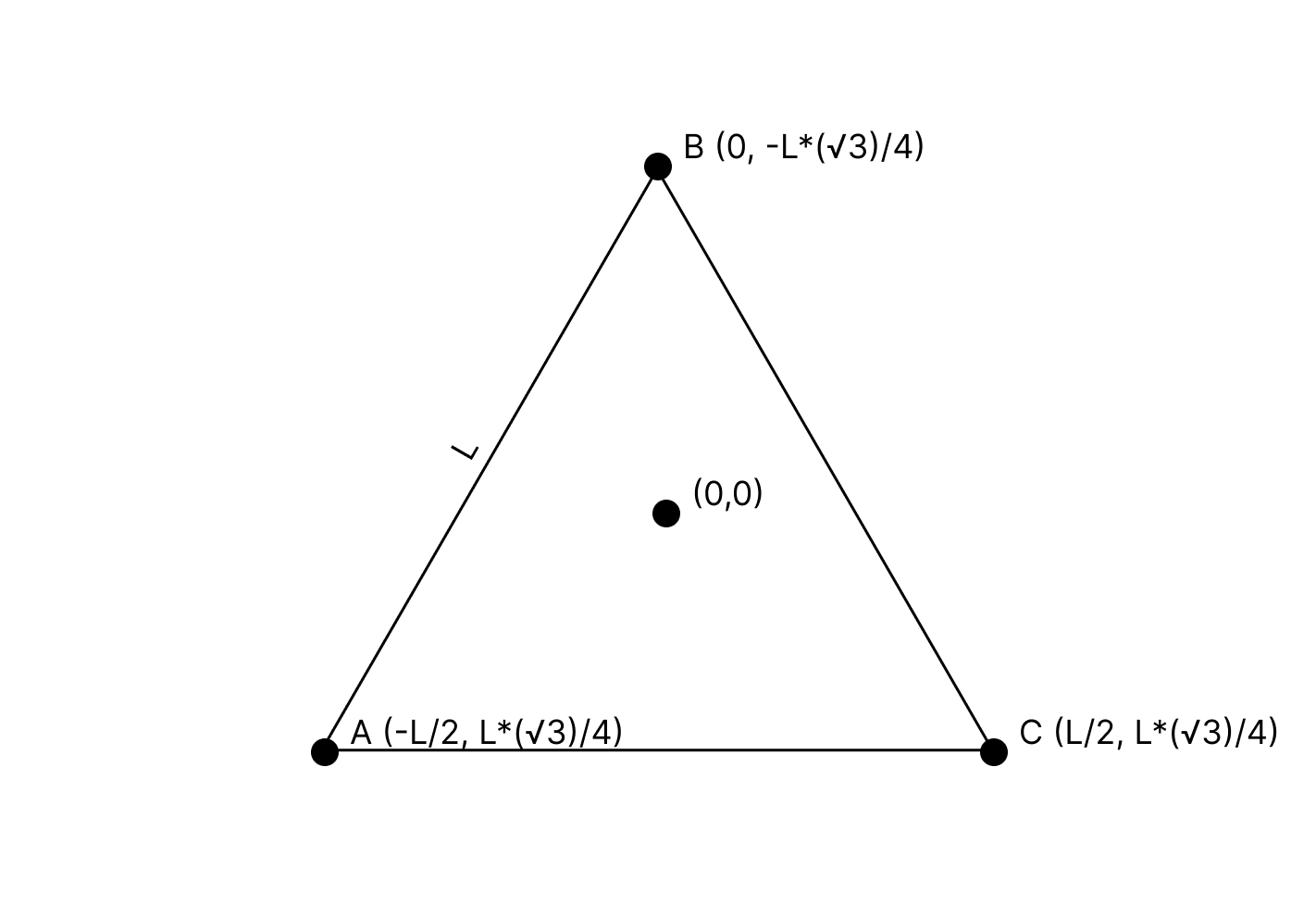
ctx.clearRect(0, 0, 50, 50) // Clears the canvas at the point (0, 0) extending 50 wide right and 50 high right down.

Drawing an equilateral triangle

To draw an equilateral triangle with with length $L$ around the origin, we first calculate out its three vertices:

$$ A = (-\frac{L}{2}, \frac{L\sqrt{3}}{4}) $$ $$ B = (0, -\frac{L\sqrt{3}}{4}) $$ $$ C = (\frac{L}{2}, \frac{L\sqrt{3}}{4}) $$

Translate this into code, and we might have something like…

let l = 10;
ctx.beginPath();
ctx.moveTo(-1 * l / 2, l * Math.sqrt(3) / 4);
ctx.lineTo(0, -1 * l * Math.sqrt(3) / 4);
ctx.lineTo(-1 * l / 2, l * Math.sqrt(3) / 4);
ctx.moveTo(-1 * l / 2, l * Math.sqrt(3) / 4);
ctx.closePath();

We can further simplify this if we say that all triangle operations are derived from the bottom left corner A. Since it is an equilateral triangle, we can derive all other vertices from here!

let l = 10;
let ax = -1 * l / 2;
let ay = l * Math.sqrt(3) / 4;

ctx.beginPath();
ctx.moveTo(ax, ay);
ctx.lineTo(ax + l / 2, ay - l * Math.sqrt(3) / 2);
ctx.lineTo(ax + l, ay);
ctx.lineTo(ax, ay);
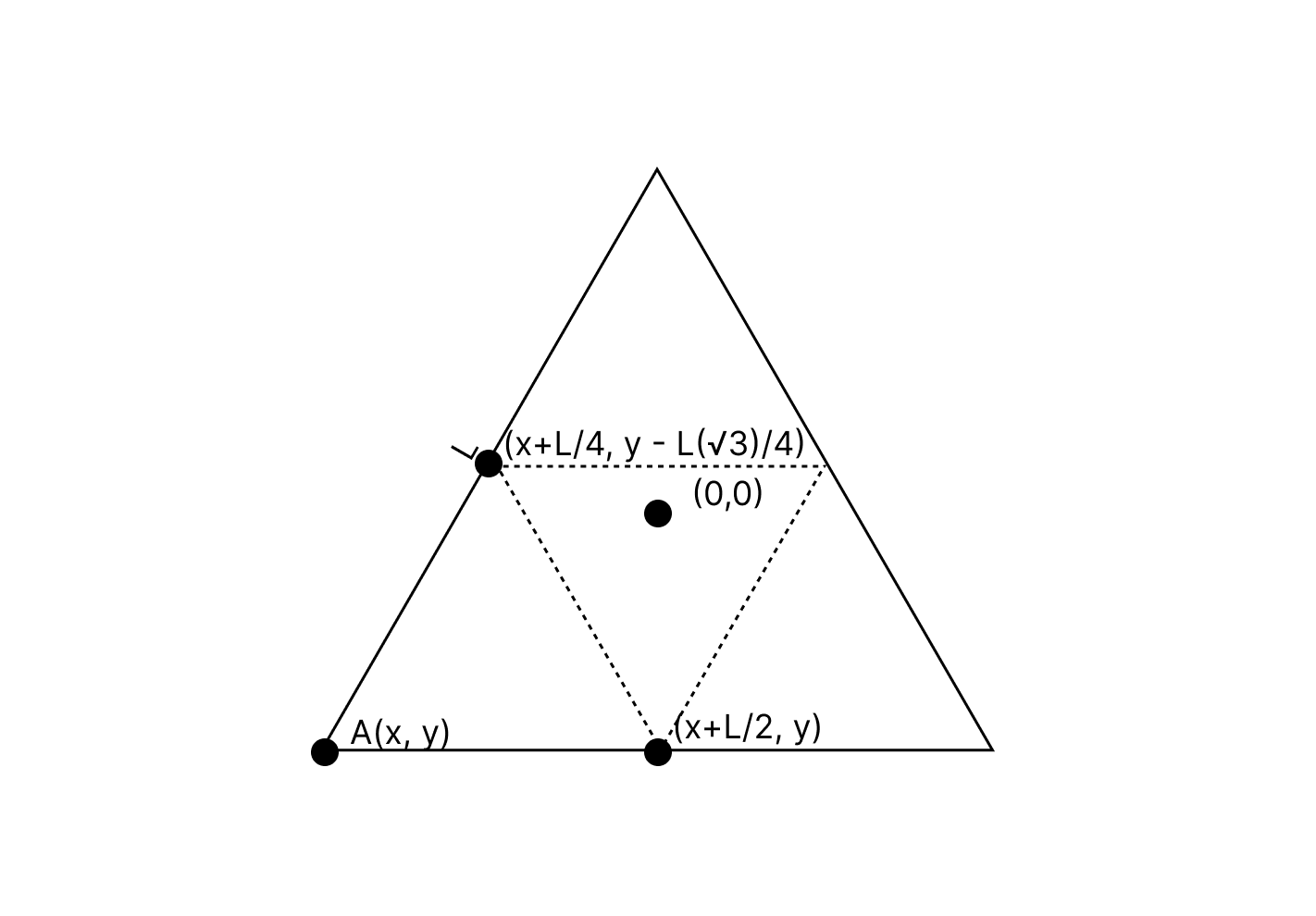
ctx.closePath();

Recursion

We begin at a certion number of iterations. At each level of recursion, we decrease the level of iteration by 1 until we hit 0. When i = 0, this is the stop condition and this is also when we draw the triangle for that subdivision. If we don’t hit the stop condition, we recursively call the draw function with coordinates for the bottom left corner of the three triangles (bottom left, top, bottom right), halving the lengths and decreasing the iteration level. The above image can help visualize this. In pseudocode, we would have the following structure:

render(iterations) {
  // Clear canvas
  // Determine the coordinates for A based on the center of the canvas
  // Draw the triangles with draw(Ax, Ay, length, iterations) — length is defined in the constructor
}

draw(x, y, length, iterations) {
  // If iterations == 0 
  // Draw the triangle
  // Else
  // Draw the bottom left triangle
  // Draw the top triangle 
  // Draw the bottom right triangle
}

At each level of recursion, when draw() is called again, we halve the length, and also decrease the iteration count.