Line Integral Convolution for Python, written in Rust
rLIC (pronounced 'relic') is a highly optimized, minimal implementation of the
Line Integral
Convolution algorithm
for in-memory numpy arrays, written in Rust.
rLIC is currently in beta. As of version 0.5.0, the only public API,
rlic.convolve, is considered feature complete and stable. However, minor
behavior changes may still happen, particularly where performance can be
improved as a result. The library as a whole may still grow additional APIs,
which wouldn't immediately be marked as stable.
rlic.convolve is trivially thread-safe, because it does not mutate any external
data. As of version 0.5.1, Wheels are not yet distributed for free-threaded
CPython, but this build target is still supported and tested.
python -m pip install rLIC
rLIC consists in a single Python function, rlic.convolve, that convolves a
texture image (usually noise) with a 2D vector field described by its
components u and v, via a 1D kernel array. The result is an image where
pixel intensity is strongly correlated along field lines.
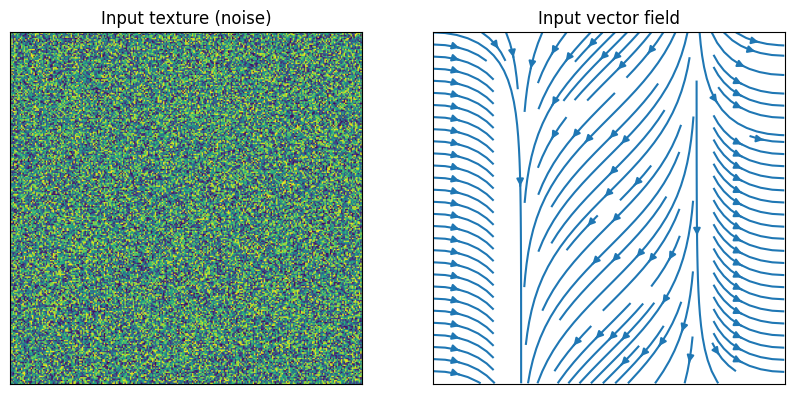
Let's see an example. We'll use matplotlib to visualize inputs and outputs.
import matplotlib.pyplot as plt
import numpy as np
import rlic
SHAPE = NX, NY = (256, 256)
prng = np.random.default_rng(0)
texture = prng.random(SHAPE)
x = np.linspace(0, np.pi, NY)
U = np.broadcast_to(np.cos(2 * x), SHAPE)
V = np.broadcast_to(np.sin(x).T, SHAPE)
fig, axs = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(10, 5))
for ax in axs:
ax.set(aspect="equal", xticks=[], yticks=[])
ax = axs[0]
ax.set_title("Input texture (noise)")
ax.imshow(texture)
ax = axs[1]
ax.set_title("Input vector field")
Y, X = np.mgrid[0:NY, 0:NX]
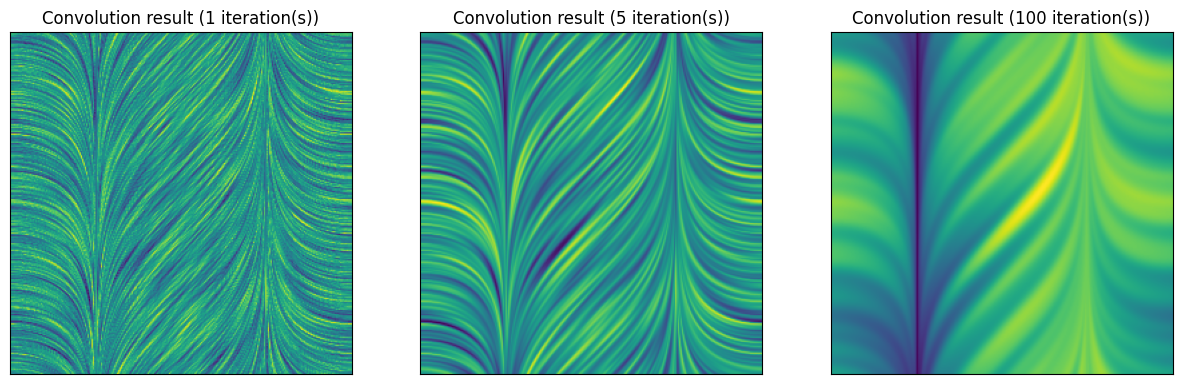
ax.streamplot(X, Y, U, V)Now let's compute some convolutions, varying the number of iterations
kernel = 1 - np.abs(np.linspace(-1, 1, 65))
fig_out, axs_out = plt.subplots(ncols=3, figsize=(15, 5))
for ax in axs_out:
ax.set(aspect="equal", xticks=[], yticks=[])
for n, ax in zip((1, 5, 100), axs_out, strict=True):
image = rlic.convolve(
texture,
U,
V,
kernel=kernel,
boundaries="periodic",
iterations=n,
)
ax.set_title(f"Convolution result ({n} iteration(s))")
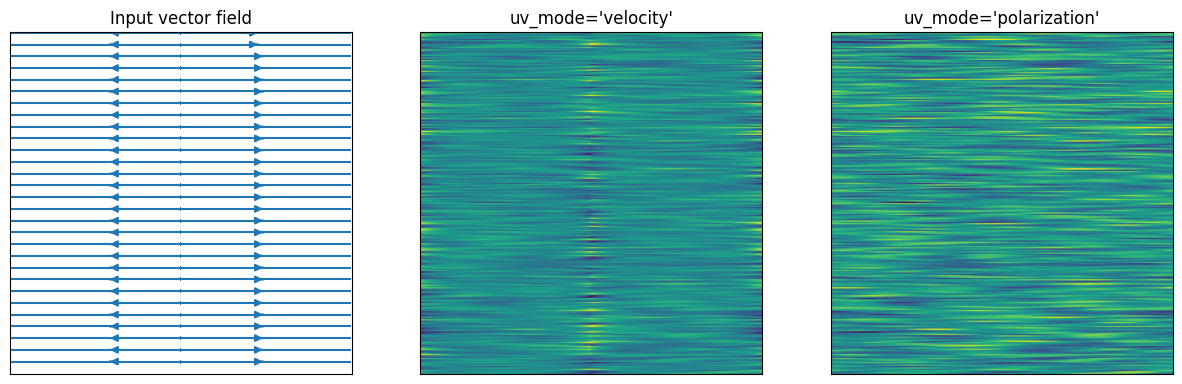
ax.imshow(image)By default, the direction of the vector field affects the result. That is, the
sign of each component matters. Such a vector field is analogous to a velocity
field. However, the sign of u or v may sometimes be irrelevant, and only
their absolute directions should be taken into account. Such a vector field is
analogous to a polarization field. rLIC supports this use case via an
additional keyword argument, uv_mode, which can be either 'velocity'
(default), or 'polarization'. In practice, the difference between these two
modes in only visible around sharps changes in sign in either u or v, and
with certain kernels.
Let's illustrate one such case
import matplotlib.pyplot as plt
import numpy as np
import rlic
SHAPE = NX, NY = (256, 256)
prng = np.random.default_rng(0)
texture = prng.random(SHAPE)
kernel = 1 - np.abs(np.linspace(-1, 1, 65, dtype="float64"))
U0 = np.ones(SHAPE)
ii = np.broadcast_to(np.arange(NX), SHAPE)
U = np.where(ii<NX/2, -U0, U0)
V = np.zeros((NX, NX))
fig, axs = plt.subplots(ncols=3, sharex=True, sharey=True, figsize=(15, 5))
for ax in axs:
ax.set(aspect="equal", xticks=[], yticks=[])
ax = axs[0]
ax.set_title("Input vector field")
Y, X = np.mgrid[0:NY, 0:NX]
ax.streamplot(X, Y, U, V)
for uv_mode, ax in zip(("velocity", "polarization"), axs[1:], strict=True):
image = rlic.convolve(
texture,
U,
V,
kernel=kernel,
uv_mode=uv_mode,
boundaries={"x": "periodic", "y": "closed"},
)
ax.set_title(f"{uv_mode=!r}")
ax.imshow(image)rLIC.convolve allocates exactly two buffers with the same size as texture,
u and v, regardless of the number of iterations performed, one of which is
discarded when the function returns. This means that peak usage is about 5/3 of
the amount needed to hold input data in memory, and usage drops to 4/3 on
return.