Diffusion models learn a generative reverse process by inverting a fixed forward noising process. Language models based on this idea can benefit from properties of diffusion: sampling is parallelizable, and the generation process can be conditioned. For example, one can initialise the process from a partial sequence and sample infillings consistent with a learned distribution. They are also able to learn structural constraints, which can be benefitial for certain domains where global consistency is important, such as source code.
This repo contains a self-contained, mostly from-scratch reimplementation of the Score Entropy Discrete Diffusion (SEDD) model from Lou et al. (2023).
This implementation focuses on clarity, and implements the forward process specialized to an absorbing transition matrix. Sampling of a random timestamp, perturbation of the sequence, and other computations needed to evaluate the integral in the objective are part of the loss function, which can be found in loss.py.
reverse.py implements a batched version of the Tweedie
The encoder-only transformer in the score network is significantly simplified, using a sinusoidal positional embedding and a simple MLP time embedding (score.py). It takes
The same log-linear noise schedule from the original implementation is used, such that
Let
We define
Let
and all mass accumulates in the absorbing state as
The model is trained to estimate unnormalized transition ratios (or, scores)
For the loss function, defining
this gives a transition operator on sequences where only one nonabsorbing token changes to the absorbing token at each step. The process cannot transition directly between nonabsorbing tokens: instead, all transitions pass through the absorbing state.
Let
where
At inference time, we use
The reverse transition probability for each position
Since
making the process computationally tractable.
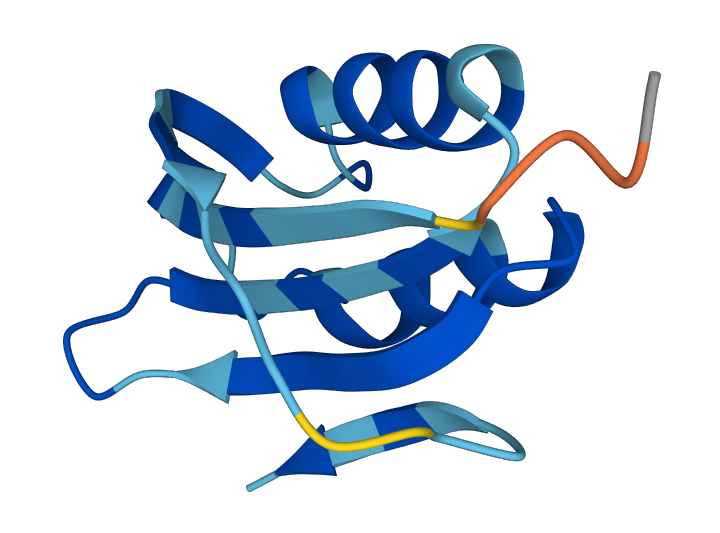
We apply the model to the ACYP protein dataset - credit for this idea goes to Alex Carlin. The dataset consists of character-level protein sequences over a 21-token alphabet, with sequence length capped at 127. Special start and end tokens are added.
Training was done for 30k steps on a single A100 GPU. Sampling used 1024 denoising steps. Folding of sampled sequences was performed using ESMFold to evaluate plausibility. Folding success was low (14 out of 300), but all successful structures were syntactically correct, suggesting the model learns the correct structural priors even without explicit folding success as part of the objective.
An example of a generated protein:
We also attempted to apply the model to the TinyStories dataset. This is currently broken for some reason (patches are welcome).