Strong, fast, simple, non-cryptography hash function
public static int mzHash32(byte[] data, int start, int length, int seed) {
int hash = 0x8979BEFC ^ seed;
for(int i = 0; i < length; i++)
hash = 0x99AF844D * ((i + data[start + i]) ^ (hash << 2) ^ (hash >>> 2));
return hash;
}It has an absolutely uniform, chaotic distribution of hash values independent of the number, length and type of input values.
It also has a good Avalanche Effect property: even a minimal differences (1 bit) of input values produces very different hash values.

Hash funtion: java.lang.String.hashCode()
Source file: words_en.txt
Distinct words: 65503
Data length = 262012 bytes
Average byte frequency = 1023.48
Minimum byte frequency = 797
Maximum byte frequency = 8727
Variance = 282898.28
Standard Deviation = 531.88
Coefficient of Variation = 51.97%
Chi-Square Test = 70760.20
Average bytes value = 120.73 (127.5 random)
Entropy = 7.9119 bits (8 random)
Monte Carlo for Pi 2D = 3.210497 (error = 2.193%)
Monte Carlo for Pi 3D = 3.360676 (error = 6.974%)
Average of Contiguous Byte Pairs = 31027.8356 (32767.5 random) (error 5.309%)
4 Bytes Collisions = 118 (expected collisions = 0.4995)

Hash funtion: mzHash32()
Source file: words_en.txt
Distinct words: 65503
Data length = 262012 bytes
Average byte frequency = 1023.48
Minimum byte frequency = 939
Maximum byte frequency = 1104
Variance = 956.08
Standard Deviation = 30.92
Coefficient of Variation = 3.02%
Chi-Square Test = 239.14
Average bytes value = 127.65 (127.5 random)
Entropy = 7.9993 bits (8 random)
Monte Carlo for Pi 2D = 3.136942 (error = 0.148%)
Monte Carlo for Pi 3D = 3.125927 (error = 0.499%)
Average of Contiguous Byte Pairs = 32807.079 (32767.5 random) (error 0.121%)
4 Bytes Collisions = 0 (expected collisions = 0.4995)
mzHash32 produces a very low number of collisions for each reasonably large number of distinct values; it is close to the collisions number of a Universal Hash Function.
The number is given by the formula n-m*(1-((m-1)/m)^n) where n is the number of input values, m is the number of all possible hash values (2^32 or 2^64).
| Data input | #Vaues | #Expected Collisions | mzHash32 | Murmur3 | XX |
|---|---|---|---|---|---|
| File words_en.txt | 65,503 | 0.5 | 0 | 0 | 0 |
| File words_es.txt | 74,571 | 0.6 | 1 | 2 | 0 |
| File words_latin.txt | 80,007 | 0.7 | 1 | 1 | 1 |
| File words_it.txt | 117,558 | 1.6 | 2 | 0 | 2 |
| File words_en_es_it_latin.txt | 315,198 | 11.6 | 11 | 9 | 9 |
| File words_and_numbers.txt | 429,187 | 21.4 | 19 | 20 | 19 |
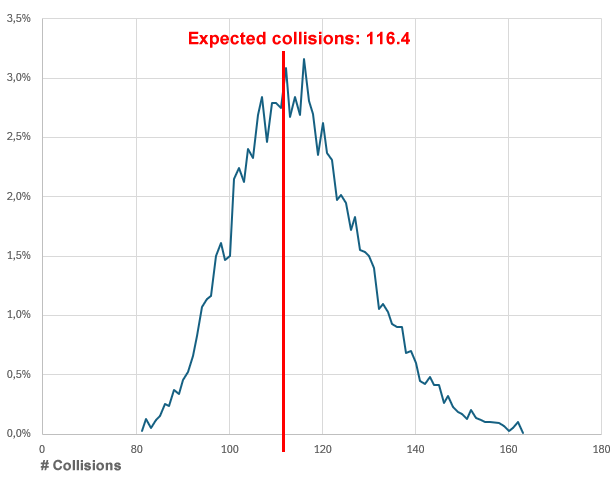
| File first_million_primes.txt | 1,000,000 | 116.4 | 118 | 118 | 85 |
| File random_64_signed_nums.txt | 1,000,000 | 116.4 | 115 | 110 | 143 |
| Numbers in english from "zero" to "nine million nine hundred ninety-nine thousand nine hundred ninety-nine" | 10,000,000 | 11,633 | 11,736 | 11,672 | 11,474 |
| File rockyou.txt dictionary of common passwords | 14,344,391 | 23,927 | 23,951 | 24,206 | 23,895 |
| Numbers in english from "five hundred thirty-nine billion four hundred ten million seven hundred one thousand four hundred eighty-three" to "five hundred thirty-nine billion four hundred twenty million seven hundred one thousand four hundred eighty-two" | 10,000,000 | 11,633 | 11,568 | 11,612 | 11,539 |
| Number as strings from "1234567890123456789" to "1234567890223456788" |
100,000,000 | 1,155,171 | 1,150,718 | 1,155,789 | 808,693 |
| Strings from "abcdefg1234567890 123456789hijklmn" to "abcdefg1234567890 223456788hijklmn" |
100,000,000 | 1,155,171 | 1,151,959 | 1,152,600 | 1,037,151 |
| Numbers as strings from "0" to "999999" | 1,000,000 | 116.4 | 117 | 120 | 17 |
| Numbers as strings from "aaaa0aaaa" to "aaaa999999aaaa" | 1,000,000 | 116.4 | 145 | 112 | 22 |
| Hex numbers as string from "0" to "98967F" | 10,000,000 | 11,633 | 10,813 | 11,433 | 2,537 |
| Data input | #Vaues | #Expected Collisions | mzHash32 | Murmur3 | XX |
|---|---|---|---|---|---|
| Binary 32 bytes random | 1,000,000 | 116.4 | 104 | 121 | 127 |
| Binary 40 bytes [b,b,b,b,b,b,b,b,b,b] b from FF676980 to FFFFFFFF | 10,000,000 | 11,633 | 11,677 | 11,695 | 11,846 |
| Binary 24 bytes [b,b,b,b,b,b], b from 00000000 to 0098967F | 10,000,000 | 11,633 | 11,471 | 11,509 | 1,542 |
| Binary 24 bytes [b,b*3,b*5,b*7,b*11,b*13], b from 00000000 to 0098967F | 10,000,000 | 11,633 | 11,667 | 11,664 | 10,831 |
Note that the number of collisions of mzHash32 is always very close to the expected value; the same goes for murmur3, while XX sometimes deviates significantly from the expected value (outliers in bold).
A good non-cryptographic hash function should be robust with respect to the seed: its behavior (especially the number of collisions) shouldn't change significantly with variations in the seed.
This ensures stable performance, predictability, and a uniform distribution of hash values.
MzHash32 maintains statistical characteristics regardless of the choice of seed; the number of collisions can vary, but always within a range that ensures a uniform distribution of the output. Furthermore, the choice of seed does not affect performance.
If there are no specific needs, it is recommended to use mzHash32 with the default seed (0) as it is optimized to produce the closest possible number of collisions to the theoretically expected number, but in case of need the quality of mzHash32 remains extremely high with the choice of a different seed.
Data input: Numbers in english from "zero" to "nine hundred ninety-nine thousand nine hundred ninety-nine"
Values: 1,000,000
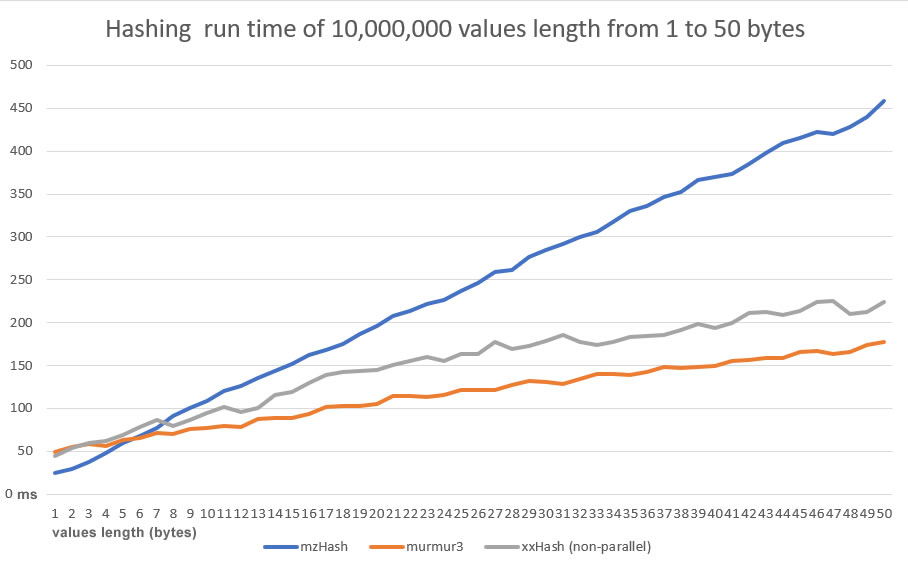
MzHash32 processes byte by byte, while Murmur and XX group 4 bytes at a time for each processing. Therefore, the speed of MzHash32 is lower, however, if the execution speed of MzHash32 is compared with other functions that process one byte at a time, it is very high-performance since the number of operations performed in each cycle is really low. The comparison obviously must be made with functions that guarantee an optimal number of collisions, close to a Universal Hash Function
MzHash32, like most non-cryptographic functions, is non-secure because it is not specifically designed to be difficult to reverse by an adversary, making it unsuitable for cryptographic purposes. Its use is instead recommended in all other contexts where hash functions are used.
Like other non-cryptographic functions, its security depends on the secrecy of the possibly used seed.
It is minimalist, elegant, straightforward and can be easily written in virtually any programming language. It produces the same result with x86 and x64 (or different) platforms. Currently C and Java versions are available.
MzHash32 demonstrates to have an excellet quality of the dispersion, close to an ideal Universal Hash Function. It is simple, portable and produces same results in all platform (x86 and x64). On the other hand it is slower than XX and Murmur3. If the goal is the quality of the dispersion and have the same result on x86 and x64 platforms, mzHash32 is certainly the function to choose!