-
Notifications
You must be signed in to change notification settings - Fork 1
01_FSM
En el desarrollo de sistemas digitales es muy habitual emplear máquinas de estado para diseñar la parte, digámoslo así, "Inteligente", que se encargará de llevar el control de los acontecimientos que irán sucediendo a lo largo del trabajo de un sistema digital, intentando que todo esté bajo control y nada se nos escape, consiguiendo que nuesrtro sistema digital haga exactamente lo que desamos y cuando lo deseamos.
Cuando se empieza a diseñar un sistema digital, tenemos una primera fase (quizás la más importante) de recoger toda la información disponible para captar con la mayor perfección posible los requerimientos que nuestro sistema digital tiene que cumplir. Una vez recopiladas las especificaciones/requerimientos que debe cumplir nuestro sistema, se emplean herramientas gráficas para poder plasmar visualmente lo que deseamos, para ello, se emplean "diagramas de flujo" que pueden ser convertidos en "diagramas de máquinas de estado" con el objetivo de ir acercándo la especificación hacia el desarrollo digital.
Una máquina de estados del tipo Moore se forma usando un estructura de grafo como la que mostramos en las siguientes figuras:


En estas imágenes podemos diferenciar las siguientes partes:
- Un "círculo" que representará el estado en el que nos encontramos en el diagrama, normalmente, se le dará un nombre al estado ( S1, estado1, subiendo, bajando ...) para identificarlo fácilmente con la operación que el sistema está realizando o el momento en el cual nuestro sistema se encuentra. Cuando lleguemos al momento de transformarlo en circuito electrónico o descripción HDL ( verilog en nuestro caso), le asignaremos una numeración. Dentro del círculo, a parte del nombre, podemos ver la "salida" que el sistema nos mostrará (qué señales de salida se activarán). En este tipo de diagrama (Moore), destacaremos que la salida será función, única y exclusivamente del estado en el que nos encontremos (independientemente del valor de las entradas recibidas ), esta es la característica a destacar de una "máquina de Moore".
- Alrededor del círculo, tendremos un conjunto de flechas que apuntan al propio círculo o salen en otra dirección (hacia otro círculo/estado), con estas flechas, se representará las transiciones/cambios de estado que pueda sufrir el sistema en función de la entrada (señal/señales de entrada) que estén presentes en ese momento. Sobre la flecha, se representa el valor que tienen las entradas en ese momento y con la flecha indicaremos hacia donde cambia/responde el estado cuando tenemos dichas entradas presentes.
A continuación, podemos ver un ejemplo de un diagrama de estado con el fin de aclarar más los conceptos explicados.
Dado un sistema compuesto de:
- Dos pulsadores A y B
- Dos leds D1 y D2
Representaremos el comportamiento que queremos que cumpla nuestro sistema al pulsar los pulsadores A y B mediante el siguiente diagrama de estado.
Se puede realizar a lápiz y papel...

O podemos usar programas como "Qfsm" para realizar diagramas de estado, inkscape u otros para dibujar dichos diagramas de estado.

En este ejemplo, se han definido cuatro posibles estados (E0,E1,E2 y E3), partimos de un estado inicial E0 e iremos cambiando de un estado a otro en función del valor obtenido en las entradas (pulsadores A y B), dependiendo del estado en el que nos encontremos, obtendremos salidas diferentes, en el estado E0 el valor obtenido en la salida será 0 (00 en binario), en E1 la salida será 1 (01 bibario), en E2 la salida será 2 (10 binario) y en el estado E3 la salida será 3 (11 binario). Recalcar que en una máquina de Moore el valor que se obtiene en las salidas depende única y exclusivamente del estado en el que nos encontremos.
Podemos representar el comportamiento en la siguiente tabla de transiciones:
| Estado Actual | (Entradas) A B | Siguiente Estado | (Salidas) D2 D1 |
|---|---|---|---|
| E0 | 0 0 | E0 | 0 0 |
| E0 | 1 0 | E1 | 0 1 |
| E0 | 0 1 | E3 | 1 1 |
| E1 | 0 0 | E1 | 0 1 |
| E1 | 1 0 | E0 | 0 0 |
| E1 | 0 1 | E2 | 1 0 |
| E2 | 0 0 | E2 | 1 0 |
| E2 | 1 0 | E3 | 1 1 |
| E2 | 0 1 | E1 | 0 1 |
| E3 | 0 0 | E3 | 1 1 |
| E3 | 1 0 | E2 | 1 0 |
| E3 | 0 1 | E0 | 0 0 |
A=1 ( equivale a pulsar el pulsador A )
B=1 ( Equivale a pulsar el pulsador B )
D1 = 1 ( Equivale a encender el Led1 )
D2 = 1 ( Equivale a encender el Led2 )
Esta tabla se leería de izquierda a derecha y de arriba hacia abajo de la siguiente forma:
-
Si estamos en el estado E0 y las entradas A B están a 0 0 el siguiente estado al que pasaríamos sería el estado E0 (nos mantenemos en el mismo estado) y el valor de las salidas Led1 Led2 serían 0 0.
-
Si estamos en el estado E0 y las entradas A B están a 1 0 el siguiente estado al que pasaríamos sería el estado E1 y el valor de las salidas Led1 Led2 serían 0 1.
-
Si estamos en el estado E0 y las entradas A B están a 0 1 el siguiente estado al que pasaríamos sería el estado E3 y el valor de las salidas Led1 Led2 sería 0 0.
-
.... (leemos de igual forma hasta llegar a la última línea de la tabla)
-
Si estamos en el estado E3 y las entradas A B están a 0 1 el siguiente estado al que pasaríamos sería el estado E0 y el valor de las salidas Led1 Led2 sería 1 1.
Como vemos en la siguiente figura, una máquina de estados la podemos dividir en 3 partes:
Figura 1

-
La parte "1", a la izquierda de la figura, estará formada por un "circuito combinacional" que recibe como entradas, el valor del "estado actual" y las señales de "entrada" del sistema a diseñar. Este circuito combinacional será el encargado de calcular el "siguiente estado" al cual irá nuestro sistema digital.
-
La parte "2", estará formada por un "circuito secuencial" que será la parte encargada de cargar el nuevo estado en el cual se encuentra el sistema, esto se realiza mediante un conjunto de biestables que serán los que den la capacidad de recordar ( memorizar ) en que estado estamos en todo momento. Los biestables se actualizarán en cada ciclo de reloj, encargándose de cargar, el estado correcto en el que nos encontramos en cada ciclo de reloj.
-
La parte "3", estará formada por un "circuito combinacional" que será la encargada de calcular las señales de salida que obtendrá el sistema. En este gráfico podemos ver dos partes "3 (3a y 3b)" ya que la salida se puede obtener siguiendo dos formas distintas, obteniendo así dos tipos de máquinas distintas, Mealy o Moore, aunque estamos tratando la máquina de Moore, se aprovecha para hacer un pequeño inciso de la máquina de Mealy ya que comparten dos partes comunes. La Máquina de Moore" se caracteriza porque las salidas se obtienen única y exclusivamente del estado actual en el que nos encontramos, por eso, este bloque 3a recibirá solo como entradas el valor del estado actual. Por otra parte, en la "Máquina de Mealy" el valor de las salidas se obtienen tanto del estado actual en el que nos encontramos como del valor de las entradas que tengamos, esta característica de la Máquina de Mealy le permite cambiar el valor de la salida de forma asíncrona, si algún valor de la entrada cambia, la salida puede que cambie de inmediato ya que el circuito combinacional de la salida (bloque 3b) responderá de inmediato ( no tiene que esperar al siguiente ciclo de reloj para reaccionar). En la máquina de Mealy realmente el bloque 3b y el bloque 1 serían el mismo bloque.
Nuestro ejemplo de la máquina de Moore, lo podemos agrupar en un módulo verilog como el que mostramos a continuación:
// Máquina de Moore
module my_moore1(clk,reset,inA,inB,OutA,OutB);
input clk,reset,inA,inB;
output OutA,OutB;
reg OutA=0,OutB=0;
reg[1:0] estado_actual=0,estado_siguiente=0;
parameter E0=0,E1=1,E2=2,E3=3; // 4 estados posibles
//********************************* Parte 1 ****************************************************************
//Parte combinacional formada por procedimiento "always @( entradas y estado_actual )" **********************
//************************************************************************************************************
always @(inA or inB or estado_actual)
begin
case(estado_actual)
E0:begin
case ({inA,inB})
0:estado_siguiente=E0;
1:estado_siguiente=E3;
2:estado_siguiente=E1;
default:estado_siguiente=E0;
endcase
end
E1:begin
case ({inA,inB})
0:estado_siguiente=E1;
1:estado_siguiente=E2;
2:estado_siguiente=E0;
default:estado_siguiente=E1;
endcase
end
E2:begin
case ({inA,inB})
0:estado_siguiente=E2;
1:estado_siguiente=E1;
2:estado_siguiente=E3;
default:estado_siguiente=E2;
endcase
end
E3:begin
case ({inA,inB})
0:estado_siguiente=E3;
1:estado_siguiente=E0;
2:estado_siguiente=E2;
default:estado_siguiente=E3;
endcase
end
default:estado_siguiente=E0;
endcase
end
// ************************** Parte 2 *****************************************************
// Parte secuencial, el estado_actual capturará el nuevo estado (estado_siguiente) ********
// ****************************************************************************************
always @(posedge clk or posedge reset)
begin
if(reset) estado_actual<=E0;
else estado_actual <= estado_siguiente;
end
// ********************** Parte 3 (3a) ************************************************************
// Parte combinacional, se asigna un valor de salida en función del estado en el que nos encontramos
//**************************************************************************************************
always @(estado_actual)
begin
case(estado_actual)
E0:{OutA,OutB}=0;
E1:{OutA,OutB}=1;
E2:{OutA,OutB}=2;
E3:{OutA,OutB}=3;
default: {OutA,OutB}=0;
endcase
end
endmodule
Este módulo lo podemos importar directamente a nuestro módulo creado en Icestudio para usarlo en un ejemplo y ver el funcionamiento de nuestra máquina de estado. La forma de añadir un fichero verilog directamente a nuestro módulo Icestudio es usando //@include fichero.v y además, dicho fichero *.v debe estar dentro del mismo directorio donde está el modulo de Icestudio.
En la siguiente figura vemos como incluimos el fichero verilog dentro de un bloque de código en icestudio.
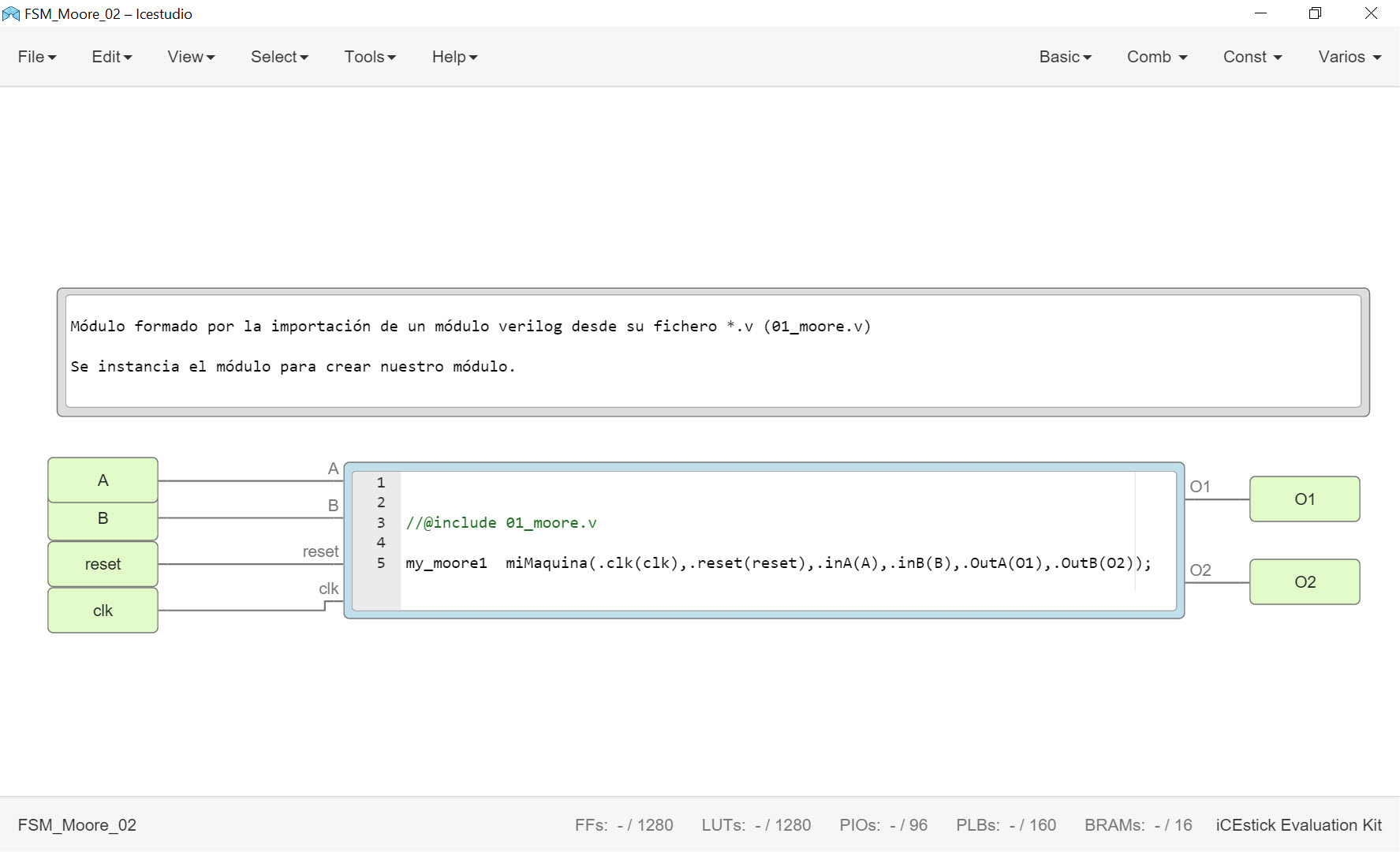
en dicho bloque creamos una instancia del módulo que contiene nuestro fichero verilog para crear el módulo que contiene la máquina de estado, creando así nuestra máquina de estado.
Realizamos un ejemplo en Icestudio donde usamos nuestra máquina de estado (Modulo_verilog) para comprobar el correcto funcionamiento, añadimos dos botones ( con sincronismo, debouncer y detector de flanco positivo crear un pulso cada vez que se pulse uno de los pulsadores ) y dos leds de salida D1, D2.

Tras cargar el ejemplo a nuestra placa ( "Icestick") podemos ver como se va cambiando de estado al ir pulsando A y B.

Hemos visto como introducir todo el fichero verilog en nuestro bloque de código Icestudio, ahora, vamos a mostrar, con el fin de verlo de forma más gráfica el mismo diseño siguiendo la estructura de la Figura 1.
Vamos a desglosar el código verilog en los tres bloques básicos comentados ( parte 1 , parte 2 y parte 3a) obteniendo el siguiente módulo en Icestudio:
Figura 2

Vamos a describir cada uno de las partes:
Este primer bloque, es un bloque combinacional que se encargará de calcular el próximo estado del sistema en función del estado actualy de las entradas que hayan presentes en ese momento.
Salida del bloque = función ( entradas, estado actual del sistema)
Para crear este bloque usameros el siguiente código verilog:
reg[1:0] estado_siguiente=0;
parameter E0=0,E1=1,E2=2,E3=3; // 4 estados posibles
//********************************* Parte 1 ****************************************************************
//Parte combinacional formada por procedimiento "always @( entradas y estado_actual )" **********************
//************************************************************************************************************
always @(inA,inB,estado_actual)
begin
case(estado_actual)
E0:begin
case ({inA,inB})
0:estado_siguiente=E0;
1:estado_siguiente=E3;
2:estado_siguiente=E1;
default:estado_siguiente=E0;
endcase
end
E1:begin
case ({inA,inB})
0:estado_siguiente=E1;
1:estado_siguiente=E2;
2:estado_siguiente=E0;
default:estado_siguiente=E1;
endcase
end
E2:begin
case ({inA,inB})
0:estado_siguiente=E2;
1:estado_siguiente=E1;
2:estado_siguiente=E3;
default:estado_siguiente=E2;
endcase
end
E3:begin
case ({inA,inB})
0:estado_siguiente=E3;
1:estado_siguiente=E0;
2:estado_siguiente=E2;
default:estado_siguiente=E3;
endcase
end
default:estado_siguiente=E0;
endcase
end
Con esta primera parte del código formamos nuestro bloque en Icestudio (Next_State), añadiendo las entradas y salidas necesarias:

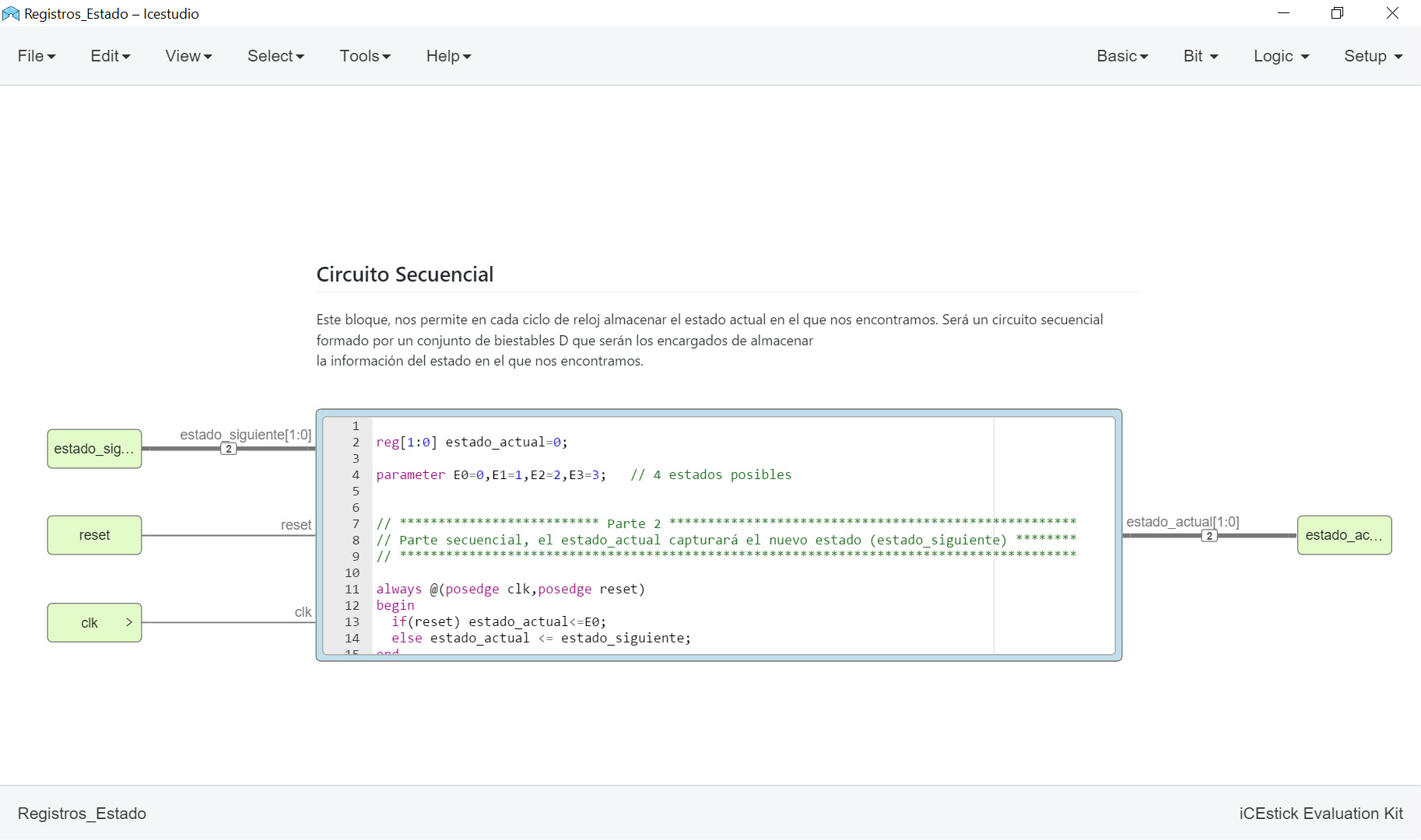
Este segundo bloque se encargará de capturar el estado_siguinente para convertirlo en el estado_actual del sistema. En resumen será un conjunto de biestables D que se encargarán de memorizar en todo momento el estado en el que se encuentra el sistema en cada ciclo de reloj.
Usaremos el siguiente código para crear nuestro bloque en Icestudio:
reg[1:0] estado_actual=0;
parameter E0=0,E1=1,E2=2,E3=3; // 4 estados posibles
// ************************** Parte 2 *****************************************************
// Parte secuencial, el estado_actual capturará el nuevo estado (estado_siguiente) ********
// ****************************************************************************************
always @(posedge clk,posedge reset)
begin
if(reset) estado_actual<=E0;
else estado_actual <= estado_siguiente;
end
Este bloque se encargará de presentar los valores correspondientes en las salidas en función única y exclusivamente del estado en el que nos encontremos (Mooore).
Salida = función (estado actual)
Usaremos el siguiente código para describir esta parte combinacional:
reg OutA=0,OutB=0;
parameter E0=0,E1=1,E2=2,E3=3; // 4 estados posibles
// ********************** Parte 3 (3a) ************************************************************
// Parte combinacional, se asigna un valor de salida en función del estado en el que nos encontramos
//**************************************************************************************************
always @(estado_actual)
begin
case(estado_actual)
E0:{OutA,OutB}=0;
E1:{OutA,OutB}=1;
E2:{OutA,OutB}=2;
E3:{OutA,OutB}=3;
default: {OutA,OutB}=0;
endcase
end

Una vez creados los tres bloques, los podemos unir conforme se muestra en la Figura 2 para formar el módulo completo que define a nuestra máquina FSM creada.

Con el cual creamos nuestro ejemplo, pudiendo grabar y probar en nuestra FPGA.

Hasta aquí, hemos visto como podemos estructurar una máquina de estados finitos por partes y tener una parte más visual de forma que sea, quizás, más fácil de comprender.