CFSpy is a package to simulate the output of a control system by means of the Chen-Fliess series.
It provides:
- The list of iterated integrals indexed by words of a certain length or less.
- The list of Lie derivatives indexed by words of a certain length or less.
- A single iterated integral indexed by a given word.
- A single Lie derivative indexed by a given word.
CFSpy is a Python library that contains the following functions:
| Function | Description |
|---|---|
| iter_int | A function for the numerical computation of a list of iterated integrals |
| iter_lie | A function for the analytical computation of a list of Lie derivatives |
| single_iter_int | A function for the numerical computation of a single iterated integral |
| single_iter_lie | A function for the analytical computation of a single Lie derivative |
CFSpy is used for:
- Simulation of the output of a control systems.
- Reachability analysis of a control system.
Currently, CFSpy supports releases of Python 3.12.4 onwards.
To install the current release:
$ pip install --upgrade CFSpyfrom CFS import iter_int, iter_lie, single_iter_int, single_iter_lie
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
import sympy as sp
# Define the Lotka-Volterra system
def system(t, x, u1_func, u2_func):
x1, x2 = x
u1 = u1_func(t)
u2 = u2_func(t)
dx1 = -x1*x2 + x1 * u1
dx2 = x1*x2 - x2* u2
return [dx1, dx2]
# Input 1
def u1_func(t):
return np.sin(t)
# Input 2
def u2_func(t):
return np.cos(t)
# Initial condition
x0 = [1/3,2/3]
# Time range
t0 = 0
tf = 3
dt = 0.001
t_span = (t0, tf)
# Simulation of the system
solution = solve_ivp(system, t_span, x0, args=(u1_func, u2_func), dense_output=True)
# Partition of the time interval
t = np.linspace(t_span[0], t_span[1], int((tf-t0)//dt+1))
y = solution.sol(t)
# Define the symbolic variables
x1, x2 = sp.symbols('x1 x2')
x = sp.Matrix([x1, x2])
# Define the system symbolically
g = sp.transpose(sp.Matrix([[-x1*x2, x1*x2], [x1, 0], [0, - x2]]))
# Define the output symbolically
h = x1
# The truncation of the length of the words that index the Chen-Fliess series
Ntrunc = 4
# Coefficients of the Chen-Fliess series evaluated at the initial state
Ceta = np.array(iter_lie(h,g,x,Ntrunc).subs([(x[0], 1/3),(x[1], 2/3)]))
# inputs as arrays
u1 = np.sin(t)
u2 = np.cos(t)
# input array
u = np.vstack([u1, u2])
# List of iterated integral
Eu = iter_int(u,t0, tf, dt, Ntrunc)
# Chen-Fliess series
F_cu = x0[0]+np.sum(Ceta*Eu, axis = 0)
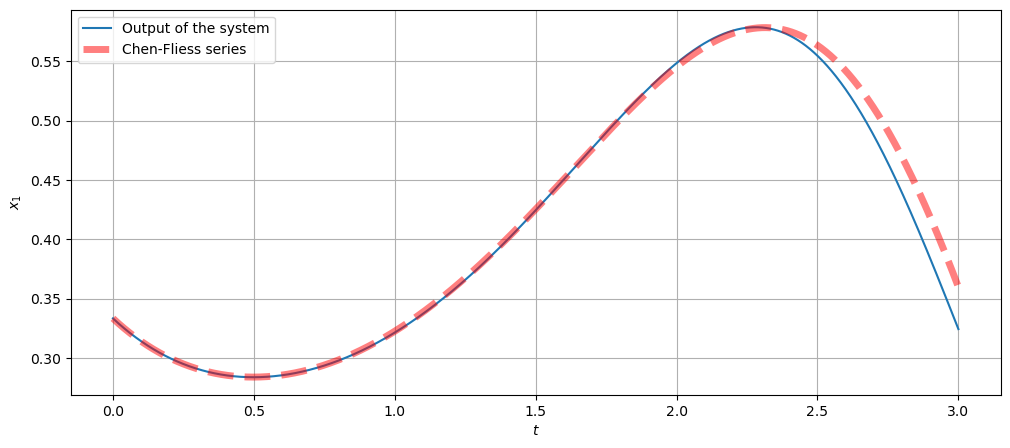
# Graph of the output and the Chen-Fliess series
plt.figure(figsize = (12,5))
plt.plot(t, y[0].T)
plt.plot(t, F_cu, color='red', linewidth=5, linestyle = '--', alpha = 0.5)
plt.xlabel('$t$')
plt.ylabel('$x_1$')
plt.legend(['Output of the system','Chen-Fliess series'])
plt.grid()
plt.show()For more examples, see the CFSpy demos
All feedback is welcome.
Please reach out if you have any questions:
CFSpy is open-source and released under the MIT License.
Feel free to cite my work:
@article{iperezave,
title={CFSpy},
author={Perez Avellaneda, Ivan},
journal={GitHub. Note: https://github.com/iperezav/CFSpy},
volume={1},
year={2024}
}