Neural PDE Solver Python Package : tf-pde

Automatic Differentiation based Partial Differential Equation solver implemented on the Tensorflow 2.x API. Package distribution under the MIT License. Built for students to get initiated on Neural PDE Solvers as described in the paper Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations.

Installation

Since the package was built as a proof-of-concept, support for it has been discontinued. However the package still works with the mentioned dependencies. We suggest running the package within a conda environment.

conda create -n TFPDE python=3.7
conda activate TFPDE
pip install tf-pde

Example(s)

To solve a particular PDE using a PINN, the package requires information on the three parameters: neural network hyperparameters, sampling parameters, information about the PDE and the case that we are solving for :

import tfpde 

#Neural Network Hyperparameters
NN_parameters = {'Network_Type': 'Regular',
                'input_neurons' : 2,
                'output_neurons' : 1,
                'num_layers' : 4,
                'num_neurons' : 64
                }


#Neural PDE Hyperparameters
NPDE_parameters = {'Sampling_Method': 'Initial',
                   'N_initial' : 300, #Number of Randomly sampled Data points from the IC vector
                   'N_boundary' : 300, #Number of Boundary Points
                   'N_domain' : 20000 #Number of Domain points generated
                  }


#PDE 
PDE_parameters = {'Inputs': 't, x',
                  'Outputs': 'u',
                  'Equation': 'D(u, t) + u*D(u, x) + 0.0025*D3(u, x)',
                  'lower_range': [0.0, -1.0], #Float 
                  'upper_range': [1.0, 1.0], #Float
                  'Boundary_Condition': "Periodic",
                  'Boundary_Vals' : None,
                  'Initial_Condition': lambda x: np.cos(np.pi*x),
                  'Initial_Vals': None
                 }

---

Partial derivative of y with respect to x is represented by D(y, x) and the second order derivative is given by D(D(y, x), x) or D2(y, x).

---

These parameters are used to initialise the model and sample the training data:

model = tfpde.main.setup(NN_parameters, NPDE_parameters, PDE_parameters)

Once the model is initiated, we determine the training parameters and solve for the PDE:

train_config = {'Optimizer': 'adam',
                 'learning_rate': 0.001, 
                 'Iterations' : 50000}

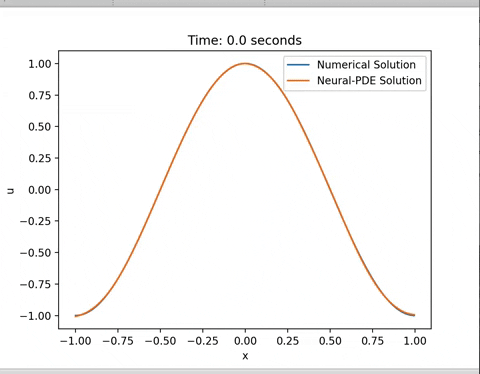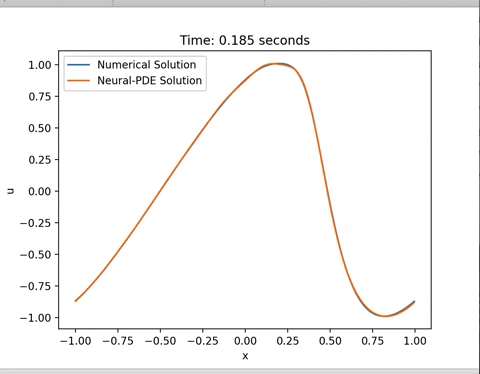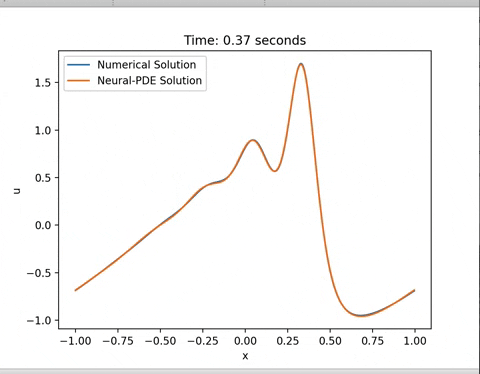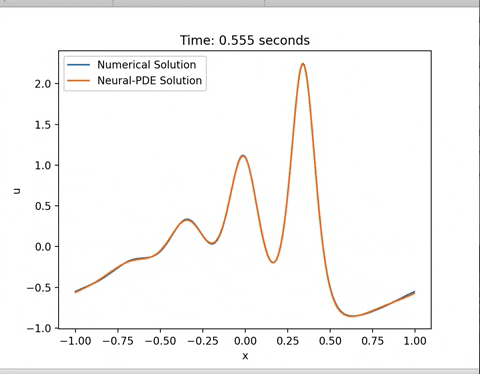
training_time = model.train(train_config, training_data)

The PDE solution can be extracted by running a feedforward operation of the trained network and compared with traditional numerical methods:

u_pred = model(X_star)

In order to gain a more theoretical understanding of the methods involved, do go through this video :