platonic-rotation 🤔

introduction

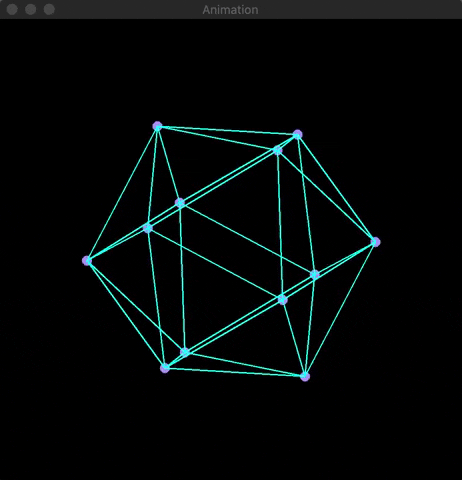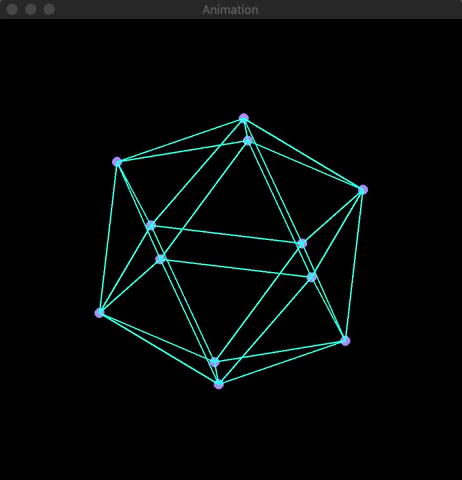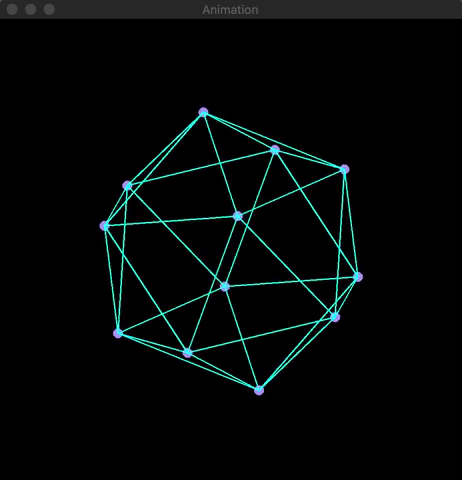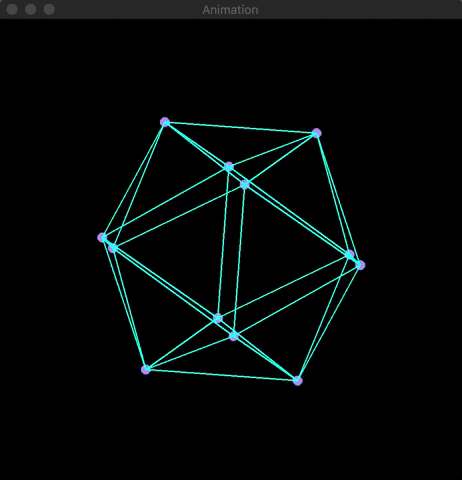
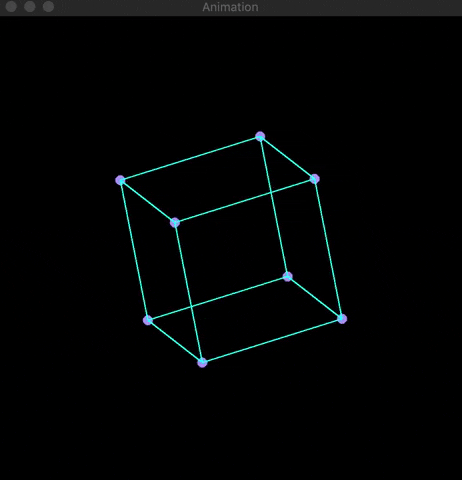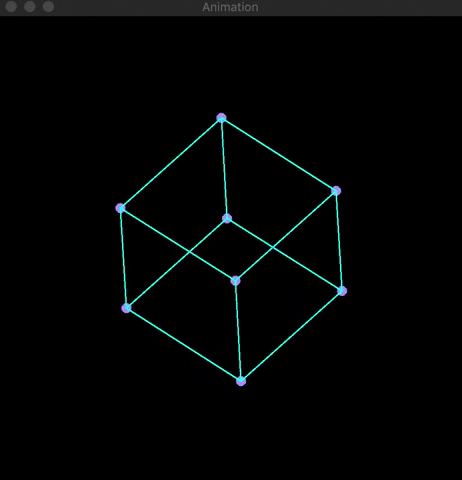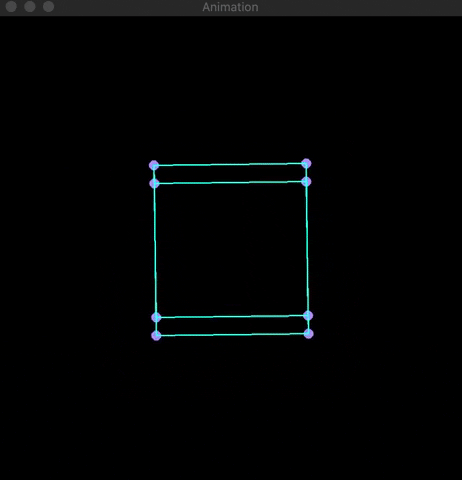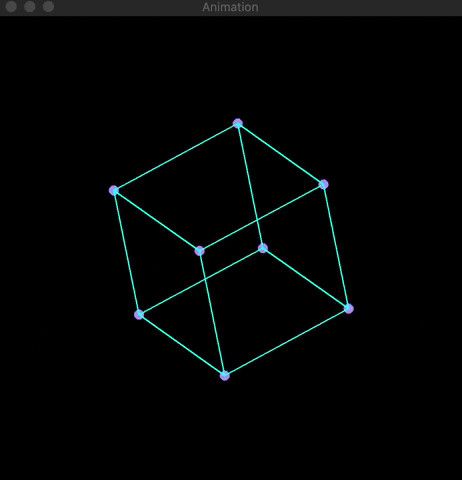
At the root of 3D rendering is the usage of basic matrix multiplication to convert three-dimensional points (x,y,z) into two-dimensional coordinates (x,y). Using OpenCV, I developed a visualization of the application of projection and rotation matrices on four platonic solids (cube, octahedron, isocadehron, & dodecahedron). Knowledge of matrix mulitplication is needed to understand the math below.

what it does

Using OpenCV's line(...) and circle(...) built-in functions along with the Mat array class, I was able to create a visualization of the platonic solid's rotation. Examples are shown below:

the math

step one: rotation

For each x-y-z coordinate, I converted the coordinate into a 1x3 matrix and then multiplied it by the following matrices.

These matrices along with three-dimensional coordinate matrix are represented in my code as two-dimensional vectors as shown here:

vector<vector<float>> rotationX{{1,0,0},{0,cos(angle),-sin(angle)},{0,sin(angle),cos(angle)}};

vector<vector<float>> rotationY{{cos(angle),0,-sin(angle)},{0,1,0},{sin(angle),0,cos(angle)}};

vector<vector<float>> rotationZ{{cos(angle),-sin(angle),0},{sin(angle),cos(angle),0},{0,0,1}};

The order of the multiplication changes how the figure rotates in the animation. In my code, I first multiplied by the Y rotation matrix, then the X rotation matrix, and finally, the Z rotation matrix as shown below:

vector<vector<float>> rotated = matmul(rotationY,points[i]); //rotates along Y axis

rotated = matmul(rotationX,rotated); //then rotated along X axis

rotated = matmul(rotationZ,rotated); //last rotated along Z axis

step two: orthographic projection

Lastly, I used the following matrix expression to convert the 1x3 x-y-z coordinate matrix into two-dimensional coordinates.

The orthogonal projection matrix is represented in my code as shown here:

vector<vector<float>> projection{{1,0,0},{0,1,0}};

run my code (for mac/linux)

In order to excute the code you must have OpenCV set up on your personal computer. Refer to here for OpenCV installation instructions. Make sure that your opencv.pc file is located in your pkgconfig folder.

In order to compile the code on your machine, cd into the cloned repo and run the following command in terminal:

g++ $(pkg-config --cflags --libs opencv) -std=c++11  [name of file].cpp -o run

Next, to run the program, enter the following command:

./run

sources

• https://en.wikipedia.org/wiki/Rotation_matrix
• https://en.wikipedia.org/wiki/3D_projection