Algorithm Complexities - Notes
| Algorithm Type | Algorithm | Best Case | Average Case | Worst Case | Space Complexity |
|---|---|---|---|---|---|
| Searching | Linear Search | O(1) | O(n) | O(n) | O(1) |
| Binary Search | O(1) | O(log n) | O(log n) | O(1) | |
| Sorting | Bubble Sort | O(n) | O(n²) | O(n²) | O(1) |
| Selection Sort | O(n²) | O(n²) | O(n²) | O(1) | |
| Insertion Sort | O(n) | O(n²) | O(n²) | O(1) | |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) | |
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) | |
| Heap Sort | O(n log n) | O(n log n) | O(n log n) | O(1) | |
| Counting Sort | O(n + k) | O(n + k) | O(n + k) | O(k) | |
| Radix Sort | O(nk) | O(nk) | O(nk) | O(n + k) | |
| Bucket Sort | O(n + k) | O(n + k) | O(n²) | O(n) | |
| Graph | BFS (Adj. List) | O(V + E) | O(V + E) | O(V + E) | O(V) |
| DFS (Adj. List) | O(V + E) | O(V + E) | O(V + E) | O(V) | |
| Dijkstra (Heap) | O((V + E) log V) | O((V + E) log V) | O((V + E) log V) | O(V + E) | |
| Bellman-Ford | O(VE) | O(VE) | O(VE) | O(V) | |
| Floyd-Warshall | O(n³) | O(n³) | O(n³) | O(n²) | |
| Kruskal’s Algorithm | O(E log E) | O(E log E) | O(E log E) | O(E + V) | |
| Prim’s Algorithm | O((V + E) log V) | O((V + E) log V) | O((V + E) log V) | O(V²) or O(E + V) with heap |
Understanding time and space complexity is crucial for optimizing algorithms. Always consider the input size and constraints to choose the most efficient algorithm.
Let me know if you need any modifications or explanations! 🚀
- অ্যালগরিদম বিশ্লেষণ
- সার্চিং অ্যালগরিদম
- সর্টিং অ্যালগরিদম
- গ্রাফ অ্যালগরিদম
- গ্রিডি অ্যালগরিদম
- ডায়নামিক প্রোগ্রামিং
- ডিভাইড অ্যান্ড কনকোয়ার
- ব্যাকট্র্যাকিং
- বিট ম্যানিপুলেশন
- উন্নত ডাটা স্ট্রাকচার
- স্ট্রিং অ্যালগরিদম
- কম্পিউটেশনাল জিওমেট্রি
- টাইম কমপ্লেক্সিটি: অ্যালগরিদমের রান টাইম নির্ধারণ করার জন্য ব্যবহৃত হয়। এটি Big-O, Big-Ω, এবং Big-Θ দ্বারা প্রকাশ করা হয়।
- স্পেস কমপ্লেক্সিটি: মেমোরি ব্যবহারের পরিমাণ বোঝায়।
- বেস্ট, এভারেজ, ওয়ার্স্ট কেস: ইনপুট ভেদে অ্যালগরিদমের পারফরমেন্স কেমন হবে তা বিশ্লেষণ করা হয়।
- Amortized Analysis: কিছু অপারেশনের গড় কমপ্লেক্সিটি নির্ধারণ করা।
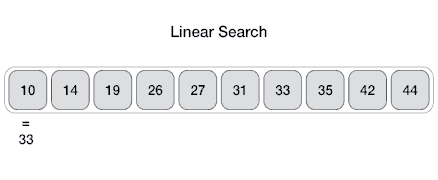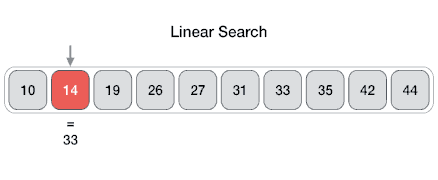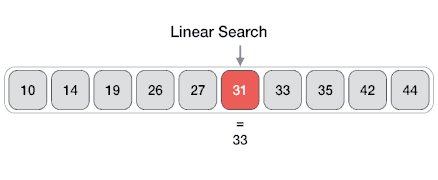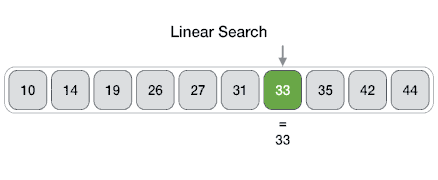
- Linear Search:
O(n)– একটি এলিমেন্ট খোঁজার জন্য পুরো লিস্টের প্রতিটি আইটেম পরীক্ষা করা হয়। - Binary Search:
O(log n)– ইনপুট লিস্ট যদি সর্টেড থাকে তবে বাইনারি সার্চ এলিমেন্ট খোঁজার জন্য দ্রুততর পদ্ধতি। - Ternary Search:
O(log n)– তিন ভাগে ভাগ করে অনুসন্ধান করা হয়। - Interpolation Search:
O(log log n)– Binary Search এর উন্নত সংস্করণ। - Exponential Search:
O(log n)– এলিমেন্টের অবস্থান অজানা হলে এটি ব্যবহার হয়।
- Bubble Sort:
O(n^2)– একের পর এক সন্নিবেশিত উপাদানগুলো তুলনা করে সর্ট করা হয়। - Selection Sort:
O(n^2)– একটি ছোটতম উপাদানকে নির্বাচন করে সেটি সঠিক স্থানে রাখার পদ্ধতি। - Insertion Sort:
O(n^2)– এলিমেন্টগুলিকে একটি একটি করে ইনসার্ট করে ইনপুট অ্যারে সর্ট করা হয়। - Merge Sort:
O(n log n)– বিভাজন এবং জয়েনিং পদ্ধতি ব্যবহার করে এলিমেন্ট সাজানো হয়। - Quick Sort:
O(n log n)– পিভট এলিমেন্ট ব্যবহার করে দ্রুত সর্টিং পদ্ধতি। - Heap Sort:
O(n log n)– একটি হিপ ডাটা স্ট্রাকচার ব্যবহার করে এলিমেন্ট সর্ট করা হয়।
- DFS (Depth First Search): একটি গ্রাফের মধ্যে গভীরতার ভিত্তিতে অনুসন্ধান করা হয়।
- BFS (Breadth First Search): একটি গ্রাফের মধ্যে প্রস্থের ভিত্তিতে অনুসন্ধান করা হয়।
- Dijkstra's Algorithm: সর্বনিম্ন দূরত্বের পথে যাওয়ার জন্য ব্যবহৃত অ্যালগরিদম।
- Bellman-Ford Algorithm: নেতিবাচক ওয়েট সহ সর্বনিম্ন পথ নির্ধারণের জন্য ব্যবহৃত হয়।
- Floyd-Warshall Algorithm: সমস্ত দম্পতি নোডের মধ্যে সর্বনিম্ন পথ খোঁজার জন্য ব্যবহৃত হয়।
- Activity Selection Problem: নির্বাচিত কর্মকাণ্ডের জন্য সর্বাধিক সময়ে কাজে লাগানোর কৌশল।
- Huffman Coding: ডাটা সংকোচন পদ্ধতি যেখানে হাফম্যান ট্রি ব্যবহার করা হয়।
- Fractional Knapsack: পণ্যের ভর অনুযায়ী সর্বাধিক লাভ অর্জন করতে গ্রিডি পদ্ধতি ব্যবহৃত হয়।
- Prim's Algorithm: মিনিমাম স্প্যানিং ট্রি তৈরি করার জন্য ব্যবহৃত।
- Fibonacci Sequence: O(n) সময়ের মধ্যে ফিবোনাচ্চি সিরিজ বের করা।
- Knapsack Problem: একটি বস্তু নির্বাচন করার জন্য সর্বাধিক মূল্য নির্ধারণ করতে ব্যবহৃত হয়।
- Longest Common Subsequence: দুটি স্ট্রিংয়ের মধ্যে সবচেয়ে বড় সাধারণ সাবসিকোয়েন্স নির্ধারণ করা।
- Longest Increasing Subsequence: একধাপ বাড়ানো উপাদানগুলোর মধ্যে সবচেয়ে বড় উপসেট বের করা।
- Merge Sort: উপরের মতো, ডিভাইড অ্যান্ড কনকোয়ার পদ্ধতি ব্যবহার করে সর্টিং অ্যালগরিদম।
- Quick Sort: ইনপুট ডাটা ভাগ করে দ্রুত সর্টিং করার জন্য ব্যবহৃত।
- Binary Search: ইনপুট ডাটা ভাগ করে দ্রুত অনুসন্ধান করা হয়।
- N-Queens Problem: একটি এন-কুয়িন্সের সমস্যা সমাধান করা যেখানে কুইনদের পরস্পরকে আক্রমণ না করে বসানো হয়।
- Subset Sum Problem: একটি সাবসেট খোঁজা যা একটি নির্দিষ্ট সংখ্যা যোগফল তৈরি করে।
- Sudoku Solver: একটি সুদোকু সমস্যা সমাধান করা।
- Bitwise AND, OR, XOR: বিটওয়াইজ অপারেশন করার পদ্ধতি।
- Checking if a number is power of 2: একটি সংখ্যা ২ এর শক্তি কিনা তা চেক করা।
- Counting set bits: একটি সংখ্যার সেট বিট গণনা করা।
- Trie: একটি ট্রি ডাটা স্ট্রাকচার যা স্ট্রিং অনুসন্ধানে ব্যবহৃত হয়।
- Segment Tree: একটি অ্যারে পরিসরের জন্য দ্রুত কুইরি এবং আপডেট অপারেশন করার জন্য ব্যবহৃত হয়।
- Fenwick Tree (Binary Indexed Tree): একটি ডাটা স্ট্রাকচার যা কুইরি ও আপডেট অপারেশন কার্যকরভাবে সম্পাদন করতে ব্যবহৃত হয়।
- Disjoint Set (Union-Find): একটি ডাটা স্ট্রাকচার যা উপাদানগুলোকে সমিতি বা ক্লাসে ভাগ করতে ব্যবহৃত হয়।
- Naive Pattern Searching: একটি স্ট্রিংয়ের মধ্যে প্যাটার্ন খোঁজার সাধারণ পদ্ধতি।
- KMP (Knuth-Morris-Pratt): দ্রুত প্যাটার্ন অনুসন্ধানের জন্য একটি উন্নত পদ্ধতি।
- Rabin-Karp: হ্যাশিং ব্যবহার করে স্ট্রিং প্যাটার্ন অনুসন্ধান করা।
- Z Algorithm: স্ট্রিং প্যাটার্ন খোঁজার জন্য একটি শক্তিশালী অ্যালগরিদম।
- Convex Hull: একটি সন্নিবেশিত পয়েন্টসের মধ্যে সর্বনিম্ন আকারের বাউন্ডিং হাল্ল তৈরি করা।
- Line Intersection: দুটি লাইন একে অপরকে ছেদ করে কিনা তা যাচাই করা।
- Point in Polygon: একটি পয়েন্ট একটি বহুপদী (polygon) এর মধ্যে অবস্থিত কিনা তা পরীক্ষা করা।
Here's a detailed explanation of the Data Structures and Algorithms (DSA) topics in C++ with examples and explanations in Bangla:
Array হল একটি নির্দিষ্ট আকারের ডাটা স্ট্রাকচার যেখানে একসাথে একাধিক ডাটা স্টোর করা যায়।
#include <iostream>
using namespace std;
int main() {
int arr[] = {1, 2, 3, 4, 5}; // Array Declaration
cout << "Array Element at index 0: " << arr[0] << endl;
return 0;
}
Linked List একটি লিনিয়ার ডাটা স্ট্রাকচার, যেখানে প্রতিটি নোডে ডাটা থাকে এবং পরবর্তী নোডের পয়েন্টার থাকে।
Singly Linked List (সিঙ্গলি লিঙ্কড লিস্ট):
#include <iostream>
using namespace std;
struct Node {
int data;
Node* next;
};
int main() {
Node* head = new Node(); // Create first node
head->data = 1;
head->next = nullptr;
Node* second = new Node(); // Create second node
second->data = 2;
second->next = nullptr;
head->next = second; // Link the first node to second node
cout << "First node data: " << head->data << endl;
cout << "Second node data: " << second->data << endl;
return 0;
}#include <iostream>
using namespace std;
struct Node {
int data;
Node* prev;
Node* next;
};
int main() {
Node* head = new Node(); // Create first node
head->data = 1;
head->prev = nullptr;
head->next = nullptr;
Node* second = new Node(); // Create second node
second->data = 2;
second->prev = head;
second->next = nullptr;
head->next = second; // Link the first node to second node
cout << "First node data: " << head->data << endl;
cout << "Second node data: " << second->data << endl;
return 0;
}
ব্যাখ্যা: এখানে, Doubly Linked List তৈরি করা হয়েছে, যেখানে প্রতিটি নোডে prev এবং next পয়েন্টার রয়েছে।
#include <iostream>
using namespace std;
struct Node {
int data;
Node* next;
};
int main() {
Node* head = new Node();
head->data = 1;
head->next = head; // Circular Link
cout << "Head node data: " << head->data << endl;
return 0;
}ব্যাখ্যা: এখানে Circular Linked List তৈরি করা হয়েছে, যেখানে লাস্ট নোড আবার প্রথম নোডে সংযুক্ত থাকে।
- Stack হল একটি ডাটা স্ট্রাকচার যা LIFO (Last In First Out) নীতি অনুসরণ করে। এর মধ্যে তিনটি মূল অপারেশন রয়েছে:
- Push Operation: একটি উপাদান স্ট্যাকে প্রবেশ করা।
- Pop Operation: সর্বশেষ উপাদানটি স্ট্যাক থেকে বের করা।
- Peek/Top Operation: স্ট্যাকের শীর্ষ উপাদান দেখা।
#include <iostream>
#include <stack>
using namespace std;
int main() {
stack<int> s;
s.push(10); // Push 10
s.push(20); // Push 20
cout << "Top element: " << s.top() << endl; // Top element
s.pop(); // Pop 20
cout << "Top element after pop: " << s.top() << endl; // Top element after pop
return 0;
}- Queue হল একটি ডাটা স্ট্রাকচার যা FIFO (First In First Out) নীতি অনুসরণ করে। vEnqueue Operation: একটি উপাদান কিউতে প্রবেশ করা।
- Dequeue Operation: প্রথম উপাদানটি কিউ থেকে বের করা।
- Front Operation: কিউয়ের প্রথম উপাদান দেখা।
#include <iostream>
#include <queue>
using namespace std;
int main() {
queue<int> q;
q.push(10); // Enqueue 10
q.push(20); // Enqueue 20
cout << "Front element: " << q.front() << endl; // Front element
q.pop(); // Dequeue 10
cout << "Front element after pop: " << q.front() << endl; // Front element after pop
return 0;
}
#include <iostream>
#include <deque>
using namespace std;
int main() {
deque<int> dq;
dq.push_front(10); // Push 10 at front
dq.push_back(20); // Push 20 at back
cout << "Front element: " << dq.front() << endl; // Front element
cout << "Back element: " << dq.back() << endl; // Back element
dq.pop_front(); // Pop 10 from front
dq.pop_back(); // Pop 20 from back
return 0;
}Priority Queue হল একটি কিউ যেখানে প্রতিটি উপাদানকে একটি priority দেওয়া হয় এবং সর্বোচ্চ priority এর উপাদান প্রথমে বের হয়।
#include <iostream>
#include <queue>
using namespace std;
int main() {
priority_queue<int> pq;
pq.push(10);
pq.push(20);
pq.push(15);
cout << "Top element (Max-Heap): " << pq.top() << endl; // 20
pq.pop();
cout << "Top element after pop: " << pq.top() << endl; // 15
return 0;
}- Binary Tree (বাইনারি ট্রি):
- একটি Binary Tree হল এমন একটি ট্রি ডাটা স্ট্রাকচার যেখানে প্রতিটি নোডের সর্বাধিক দুটি সন্তান থাকতে পারে।
#include <iostream>
using namespace std;
struct Node {
int data;
Node* left;
Node* right;
};
int main() {
Node* root = new Node();
root->data = 1;
root->left = new Node();
root->right = new Node();
root->left->data = 2;
root->right->data = 3;
cout << "Root: " << root->data << endl;
cout << "Left Child: " << root->left->data << endl;
cout << "Right Child: " << root->right->data << endl;
return 0;
}- Binary Search Tree (BST) হল একটি বাইনারি ট্রি, যেখানে প্রতিটি নোডের left সন্তানের মান তার নিজের মানের চেয়ে ছোট এবং right সন্তানের মান তার নিজের মানের চেয়ে বড় হয়।
#include <iostream>
using namespace std;
struct Node {
int data;
Node* left;
Node* right;
};
Node* insert(Node* root, int value) {
if (root == nullptr) {
Node* newNode = new Node();
newNode->data = value;
newNode->left = newNode->right = nullptr;
return newNode;
}
if (value < root->data) {
root->left = insert(root->left, value);
} else {
root->right = insert(root->right, value);
}
return root;
}
int main() {
Node* root = nullptr;
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 5);
cout << "Root: " << root->data << endl; // 10
cout << "Left Child: " << root->left->data << endl; // 5
cout << "Right Child: " << root->right->data << endl; // 20
return 0;
}- Heap একটি পূর্ণ বাইনারি ট্রি যা হিপ প্রপার্টি অনুসরণ করে। এটি দুটি ধরনের হতে পারে:
- Max-Heap: যেখানে প্রতিটি নোডের মান তার সন্তানের মানের চেয়ে বড়।
- Min-Heap: যেখানে প্রতিটি নোডের মান তার সন্তানের মানের চেয়ে ছোট।
#include <iostream>
#include <queue>
using namespace std;
int main() {
priority_queue<int> maxHeap;
maxHeap.push(10);
maxHeap.push(20);
maxHeap.push(15);
cout << "Max Heap Top: " << maxHeap.top() << endl; // 20
return 0;
}######ব্যাখ্যা: এখানে Max-Heap ব্যবহার করা হয়েছে, যেখানে সর্বোচ্চ মান (20) শীর্ষে থাকে।
- Hash Table (হ্যাশ টেবিল):
- Hash Table একটি ডাটা স্ট্রাকচার যা কী-বয়সী মান সংরক্ষণ করে এবং দ্রুত অ্যাক্সেসের জন্য একটি হ্যাশ ফাংশন ব্যবহার করে।
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
unordered_map<string, int> hashTable;
hashTable["apple"] = 5;
hashTable["banana"] = 3;
cout << "Apple count: " << hashTable["apple"] << endl;
return 0;
}- বিট ম্যানিপুলেশন (Bit Manipulation) AND, OR, XOR Operations (এন্ড, অর, এক্সঅর অপারেশন):
#include <iostream>
using namespace std;
int main() {
int a = 5; // 0101
int b = 3; // 0011
cout << "a & b: " << (a & b) << endl; // AND operation
cout << "a | b: " << (a | b) << endl; // OR operation
cout << "a ^ b: " << (a ^ b) << endl; // XOR operation
return 0;
}- Union by Rank (ইউনিয়ন বাই র্যাংক):
- Union-Find ডাটা স্ট্রাকচারটি উপাদানগুলির গ্রুপিংয়ের জন্য ব্যবহার করা হয়, যেখানে দুটি সেটের ইউনিয়ন করা এবং তাদের মধ্যে কোনটি বড় তা ট্র্যাক করা হয়।
#include <iostream>
#include <vector>
using namespace std;
class DisjointSet {
public:
vector<int> parent, rank;
DisjointSet(int n) {
parent.resize(n);
rank.resize(n, 0);
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
void unite(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else {
parent[rootY] = rootX;
++rank[rootX];
}
}
}
};
int main() {
DisjointSet ds(5);
ds.unite(0, 1);
ds.unite(1, 2);
cout << "Find(0): " << ds.find(0) << endl; // 0
cout << "Find(2): " << ds.find(2) << endl; // 0
return 0;
}