• Améliorer la qualité de filtrage en augmentant l’ordre du filtre. • Appliquer un filtre numérique pour supprimer les composantes indésirables d’un signal. • Faire la synthèse d’un filtre numérique.
Il est à remarquer que ce TP traite en principe des signaux continus. Or, l'utilisation de Matlab suppose l'échantillonnage du signal. Il faudra donc être vigilant par rapport aux différences de traitement entre le temps continu et le temps discret.
Toutes les figures devront être tracées avec les axes et les légendes des axes appropriés.
un script Matlab commenté contenant le travail réalisé et des commentaires sur ce que vous avez compris et pas compris, ou sur ce qui vous a semblé intéressant ou pas, bref tout commentaire pertinent sur le TP.
%%
% Fréquence d'échantillonnage (en Hz)
fs = 1000;
% Temps (en secondes)
ts = 1/fs;
t = 0:ts:1;
% Amplitude des deux signaux sinusoïdaux
A1 = 1;
A2 = 0.5;
% Fréquence des deux signaux sinusoïdaux (en Hz)
f1 = 100;
f2 = 200;
% Génération des deux signaux sinusoïdaux
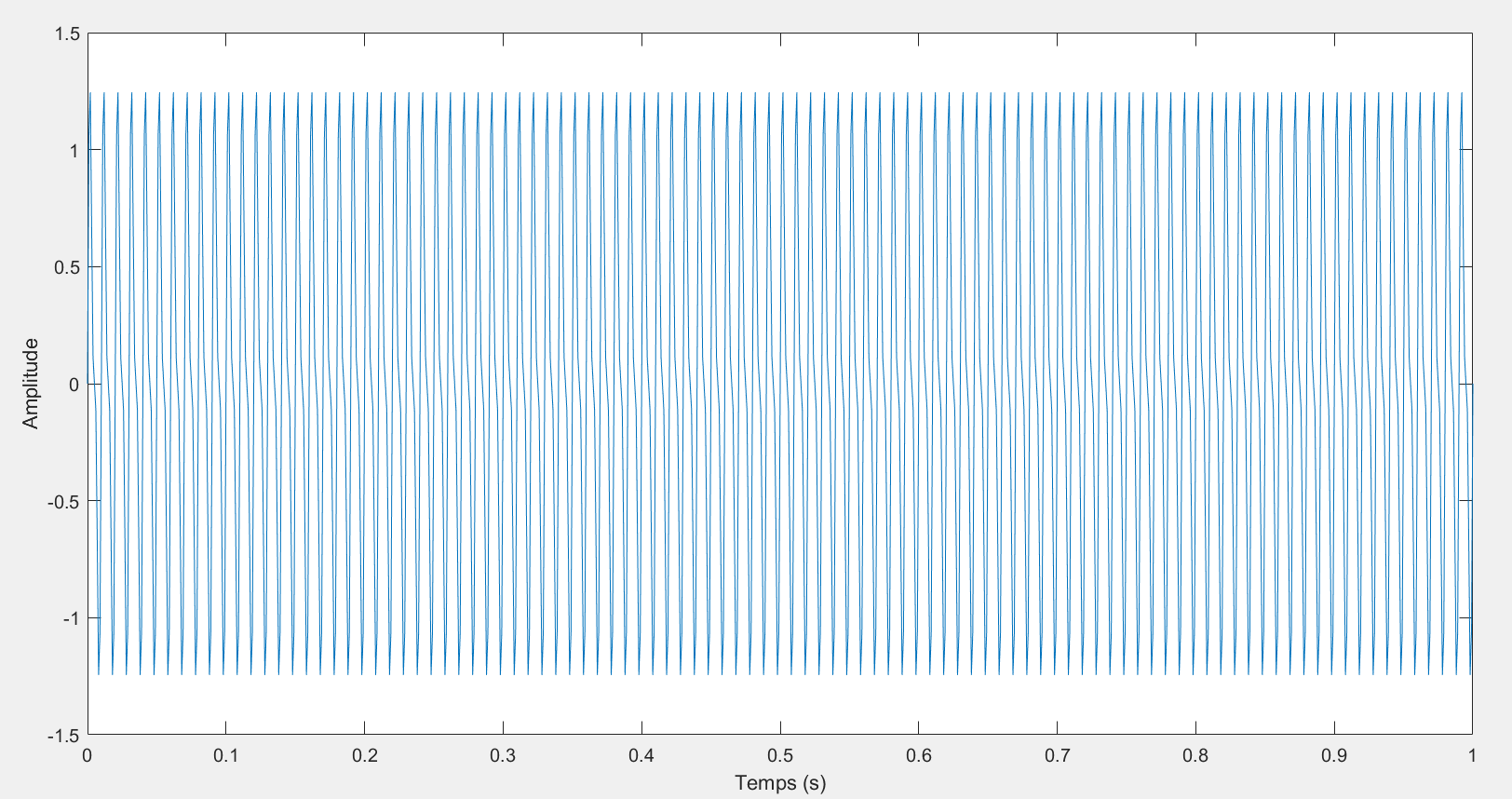
s1 = A1*sin(2*pi*f1*t);
s2 = A2*sin(2*pi*f2*t);
% Combinaison des deux signaux pour obtenir le signal s(t)
s = s1 + s2;
% Affichage du signal s(t)
plot(t, s);
xlabel('Temps (s)');
ylabel('Amplitude');
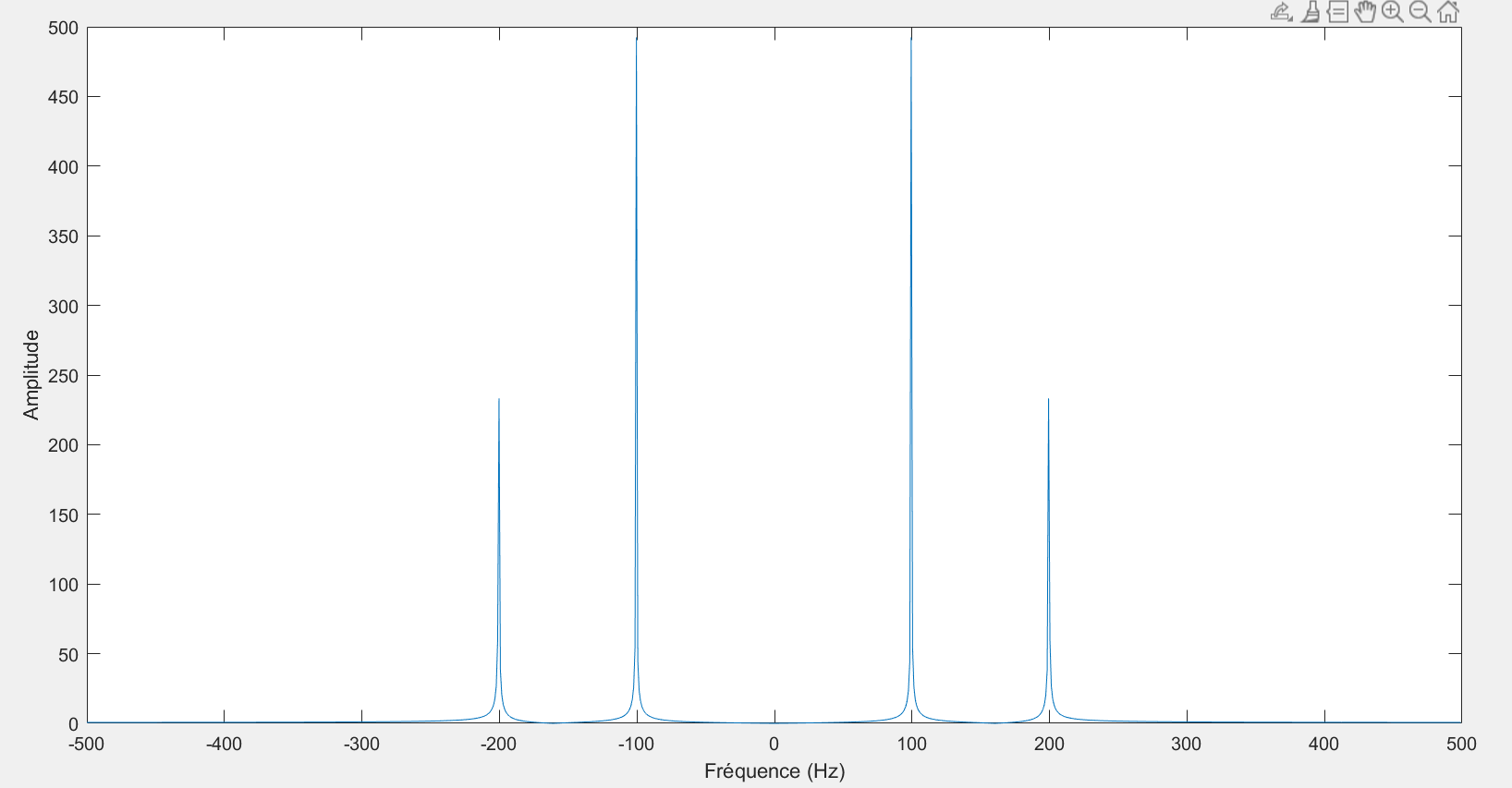
% Calcul de la fréquence (en Hz) correspondant à chaque bin
f = (0:N-1)*fs/N;
fshift = (-N/2:N/2-1)*(fs/N);
y = fft(s);
plot(fshift,fftshift(abs(y)));
xlabel('Fréquence (Hz)');
ylabel('Amplitude');
3- Créer deux filtres permettant de séparer les deux signaux. Tracer la réponse fréquentielle des filtres numériques ainsi définis.
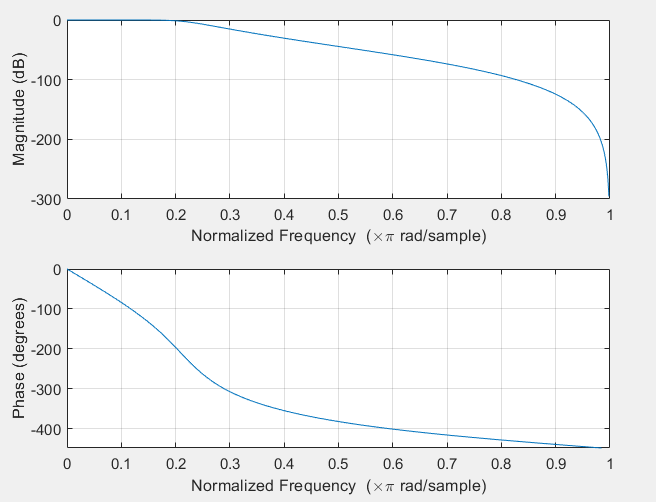
% Paramètres du filtre passe-bas
fcut = 110; % fréquence de coupure en Hz
ordre = 5; % ordre du filtre
% Création du filtre passe-bas
[b, a] = butter(ordre, fcut/(fs/2), 'low'); % la fréquence de coupure normalisée pour être comprise entre 0 et 1
% Tracer la réponse fréquentielle du filtre
freqz(b, a);==> la fonction "butter" est utilisée pour générer les coefficients d'un filtre passe-bas ou passe-haut. Cette fonction peut être utilisée pour créer un filtre numérique de Butterworth à n poles, qui est un filtre de type IIR (réponse impulsionnelle infinie)
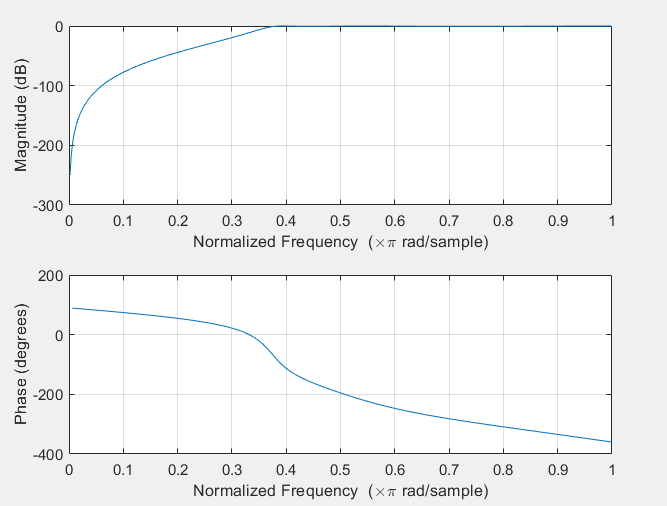
% Paramètres du filtre
f_coupure = 190; % Fréquence de coupure (en Hz)
ordre = 5; % Ordre du filtre
ripple = 0.5; % Ripple en dB %0.5 dB signifie que la perte d'atténuation peut varier de 0.5 dB dans la région de la fréquence de coupure
% Création du filtre passe-bas
[b, a] = cheby1(ordre, ripple, f_coupure/(fs/2), 'high');
freqz(b, a);==> la fonction "cheby1" est utilisée pour générer les coefficients d'un filtre passe-bas ou passe-haut à réponse en cheminement à faible ripple. Cette fonction peut être utilisée pour créer un filtre numérique de premier ordre, qui est un filtre de type IIR (réponse impulsionnelle infinie).
% Appliquer le filtre passe-bas au signal s(t)
x_filtre = filter(b, a, x);
% Calculer la TFD du signal
fft_x_filtre = fft(x_filtre);
% Obtenir la fréquence
f = (0:N-1)*fs/N;
fshift = (-N/2:N/2-1)*(fs/N);
plot(fshift,fftshift(abs(fft_x_filtre)));
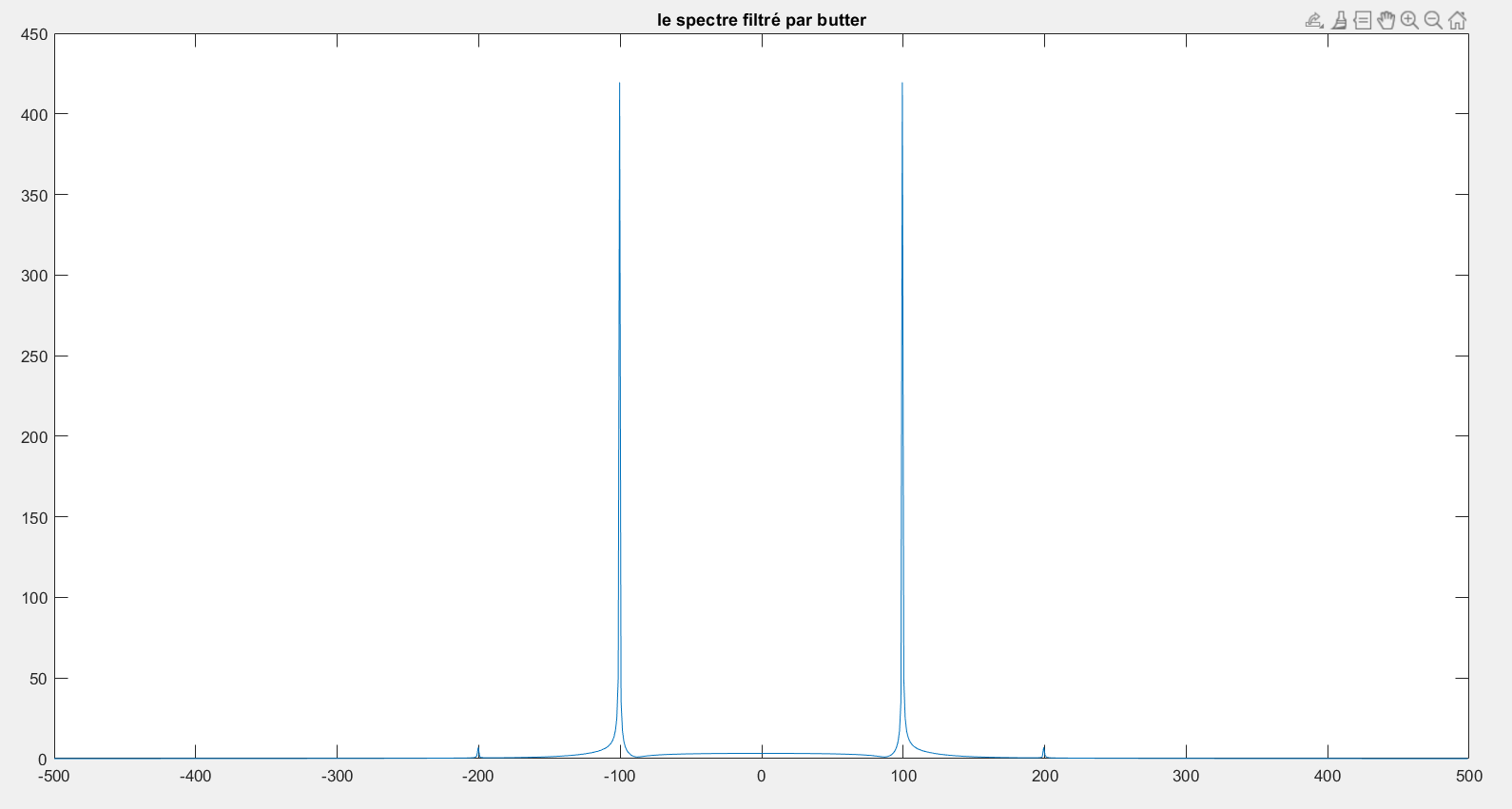
title("le spectre filtré par butter");==> la fonction "filter" est utilisé pour filtrer des signaux. Elle prend en entrée un filtre numérique et un signal à filtrer, et retourne la sortie du filtre.
% Appliquer le filtre passe-bas au signal s(t)
x_filtre = filter(b, a, x);
%plot(t,x_filtre)
% Calculer la TFD du signal
fft_x_filtre = fft(x_filtre);
% Obtenir la fréquence
f = (0:N-1)*fs/N;
fshift = (-N/2:N/2-1)*(fs/N);
plot(fshift,fftshift(abs(fft_x_filtre)));
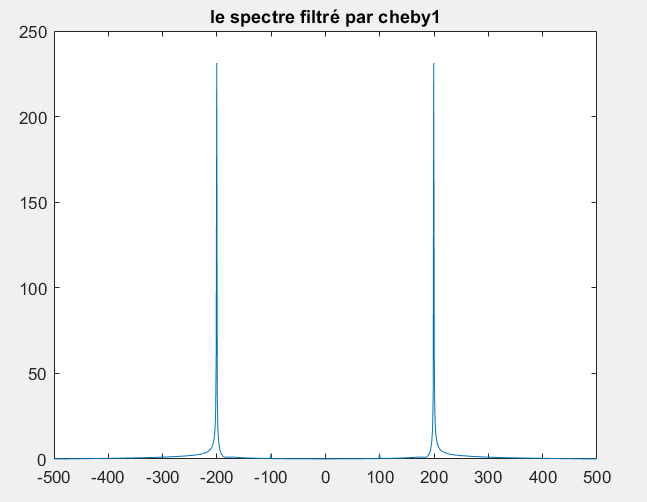
title("le spectre filtré par cheby1");5- Avec quelles caractéristiques de filtres (fréquence de coupure et ordre) obtient-on de bonnes performances de filtrage ?
[x,fe] = audioread('affreux.wav');
[x2,fe2] = audioread('akesuper.wav');N1 = length(x);
N2 = length(x2);
te1 = 1/fe;
te2 = 1/fe2;
t1 = (0:N1-1)*te1;
t2 = (0:N2-1)*te2;
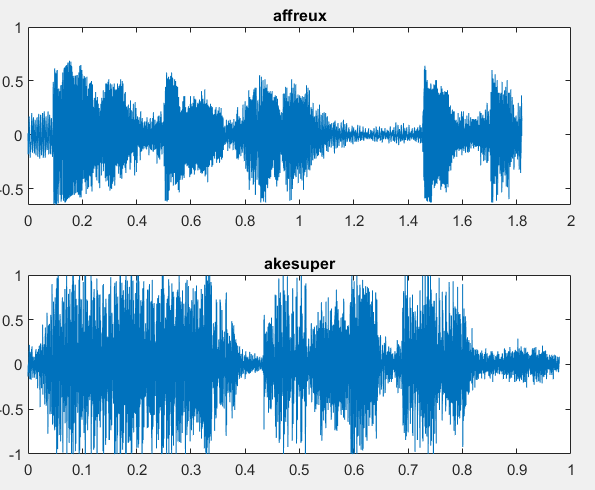
subplot(2,1,1)
plot(t1,x)
title("affreux");
subplot(2,1,2)
plot(t2,x2)
title("akesuper");
f1 =(0:N1-1)*(fe/N1); %frequence du spectre
fshift1 = (-N1/2:N1/2-1)*(fe/N1);
f2 =(0:N2-1)*(fe/N1); %frequence du spectre
fshift2 = (-N2/2:N2/2-1)*(fe/N2);
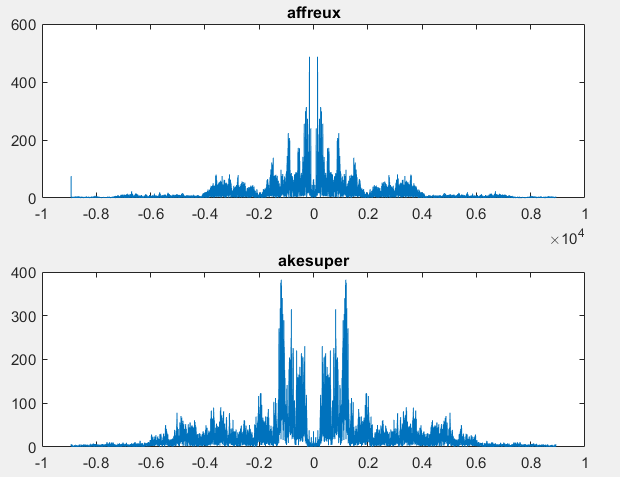
subplot(2,1,1)
y = fft(x); % y: spectre , fft(x) : transformee de fourier
plot(fshift1,fftshift(abs(y)));
title("affreux");
subplot(2,1,2)
y2 = fft(x2); % y: spectre , fft(x) : transformee de fourier
plot(fshift2,fftshift(abs(y2)));
title("akesuper");bruit1 = randn(size(x))*10^(-1);
bruit2 = randn(size(x2))*10^(-1);% génération d'un bruit blanc gaussien de -20dB
y_bruit = x + bruit1; % superposition du bruit au signal
y2_bruit= x2 + bruit2 ;freqz(b, a); % Design du filtre
fcut = 2500; % fréquence de coupure en Hz
ordre = 10; % ordre du filtr
[b,a] = butter(ordre, fcut/(fe/2), 'low'); % Filtre passe-bas de 10ème ordre avec une coupure à 0.3*fe
% Filtrage du signal bruité
y_filtre = filter(b,a,y_bruit);4- Analyser le résultat obtenu en fonction de la fréquence de coupure du filtre L’enregistrement sous format WAV d’un signal se fait avec la commande wavwrite
%enregistrement du signal filtré
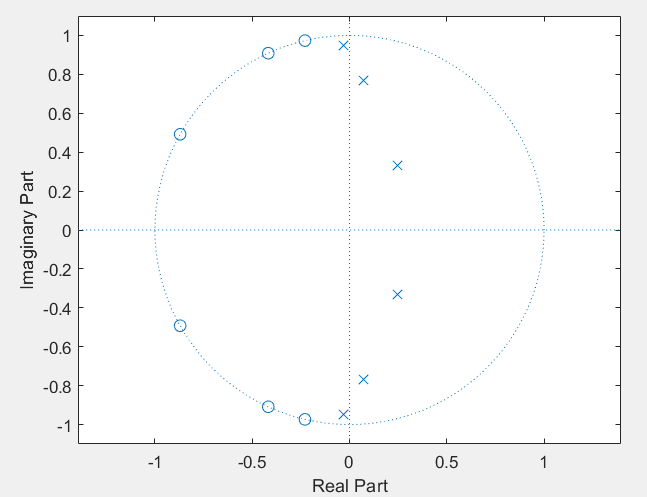
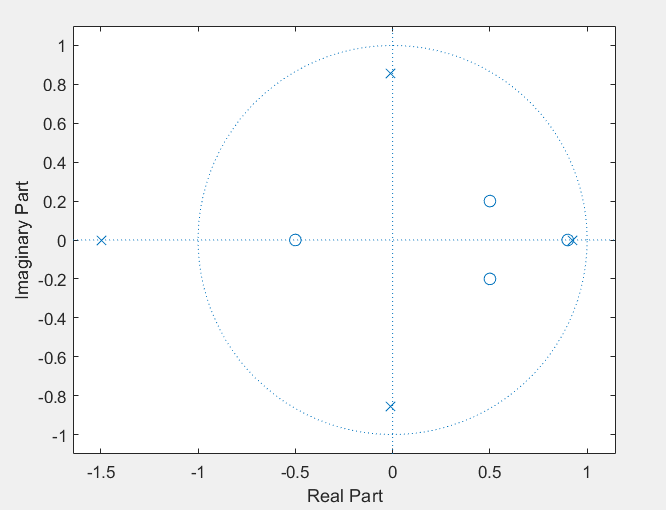
audiowrite('audy_filtre.wav',y_filtre, fe);1- Parmi les filtres IIR suivants, lequel est stable ? (Utiliser la commande roots et la commande tf2zpk, zplane)
==>La fonction "tf2zpk" permet de convertir une fonction de transfert d'un système continu, en une fonction de transfert discrète.
==>La fonction "zplane" est utilisée pour visualiser les zéros et les poles d'un filtre. Cela permet de déterminer la stabilité et les caractéristiques de fréquence d'un filtre, il affiche un diagramme de Nyquist représentant les zéros et les poles dans le plan complexe. Dont,Les zéros sont représentés par des cercles blancs et les poles par des cercles noirs. La stabilité d'un filtre peut être déterminée en examinant les positions des poles par rapport à l'unité (dans ou en dehors du cercle unité).
% Coefficients du filtre
B = [0.0725 0.2200 0.4085 0.4883 0.4085 0.2200 0.0725];
A = [1.0000 -0.5835 1.7021 -0.8477 0.8401 -0.2823 0.0924];
% Racines du polynôme caractéristique
r = roots(B);
% Vérification de la stabilité
isStable = all(real(r) <0);
if isStable
disp("Le filtre 1 est stable.")
else
disp("Le filtre 1 n'est pas stable.")
end
% Utiliser la commande tf2zpk pour convertir le filtre en forme polaire
[z,p,k] = tf2zpk(B,A); %"z" représente les zéros du filtre %"p" représente les pôles du filtre %"k" représente le gain constant du filtre.
% Utiliser la commande zplane pour tracer le plan de pole-zero
zplane(z,p);% Coefficients du filtre
B=[1.0000 1.3000 0.4900 -0.0130 -0.0290];
A=[1.0000 -0.4326 -1.6656 0.1253 0.2877];
% Racines du polynôme caractéristique
r = roots(B);
% Vérification de la stabilité
isStable = all(real(r) <0);
if isStable
disp("Le filtre 2 est stable.")
else
disp("Le filtre 2 n'est pas stable.")
end
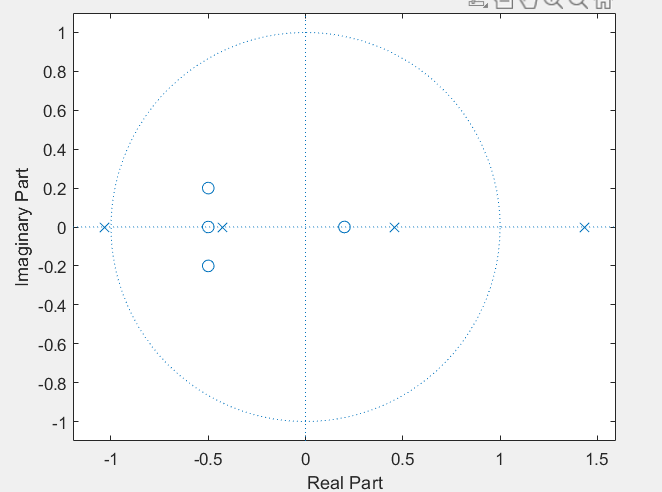
% Utiliser la commande tf2zpk pour convertir le filtre en forme polaire
[z,p,k] = tf2zpk(B,A);
% Utiliser la commande zplane pour tracer le plan de pole-zero
zplane(z,p);% Coefficients du filtre
B=[1.0000 -1.4000 0.2400 0.3340 -0.1305];
A=[1.0000 0.5913 -0.6436 0.3803 -1.0091];
% Racines du polynôme caractéristique
r = roots(B);
% Vérification de la stabilité
isStable = all(real(r) <0);
if isStable
disp("Le filtre 3 est stable.")
else
disp("Le filtre 3 n'est pas stable.")
end
% Utiliser la commande tf2zpk pour convertir le filtre en forme polaire
[z,p,k] = tf2zpk(B,A);
% Utiliser la commande zplane pour tracer le plan de pole-zero
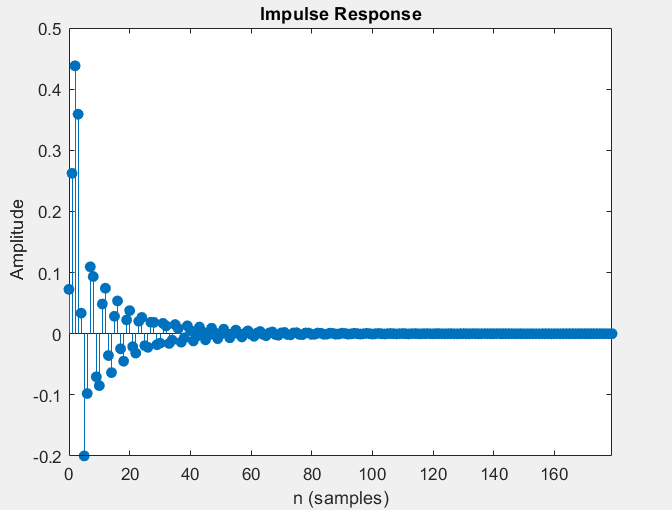
zplane(z,p);2- Vérifier que votre sélection de filtre stable est correcte en utilisant la fonction filter et en appliquant au filtre l’impulsion de Dirac comme signal d'entrée (Voir comment définir le signal impulsion de Dirac dans le cas discret). Essayer ceci sur l'un des filtres instables et observer la différence avec le filtre stable. Utiliser également la commande impz.
B=[0.0725 0.2200 0.4085 0.4883 0.4085 0.2200 0.0725];
A=[1.0000 -0.5835 1.7021 -0.8477 0.8401 -0.2823 0.0924];
% Définir l'impulsion de Dirac
d = [1, zeros(1,1000)]; % signal d'entrée
% Appliquer le filtre au signal d'entrée
y = filter(A,B, d);
N=length(d);
fe=1000;
te=1/fe;
% Utiliser la commande impz pour afficher la réponse impulsionnelle
impulsion=impz(B,A);
if abs(impulsion(end)) < 1e-5
fprintf('Le filtre est stable\n');
else
fprintf('Le filtre n''est pas stable\n');
end==> La commande "impz" est utilisée pour tracer la réponse impulsionnelle d'un filtre numérique. La réponse impulsionnelle d'un filtre donne une idée de sa réponse pour un signal d'entrée impulsion de Dirac, il prend en entrée les coefficients du filtre et retourne un graphique de la réponse impulsionnelle
3- Ecrire une fonction « transfert » qui calculera la fonction de transfert (transmittance en Z du filtre) d'un filtre IIR, et puis qui évalue cette transmittance en différentes valeurs de fréquence. L'entrée devra être les vecteurs B et A (coefficients du filtre), le nombre d’échantillons, ainsi que la période d’échantillonage. La sortie devra être la fonction de transfert complexe et ses valeurs pour les fréquences correspondantes.
function [H,H_f, freqs] = transfert(B, A, N, T)
% Calculer la fonction de transfert
H = tf(B, A);
% Calculer les fréquences pour lesquelles évaluer la transmittance
f = linspace(0, 1/(2*T), N/2);
freqs = f;
% Évaluer la transmittance pour chaque fréquence
for i = 1:length(f)
z = exp(1i*2*pi*f(i)*T);
H_f(i) = evalfr(H,z);
end
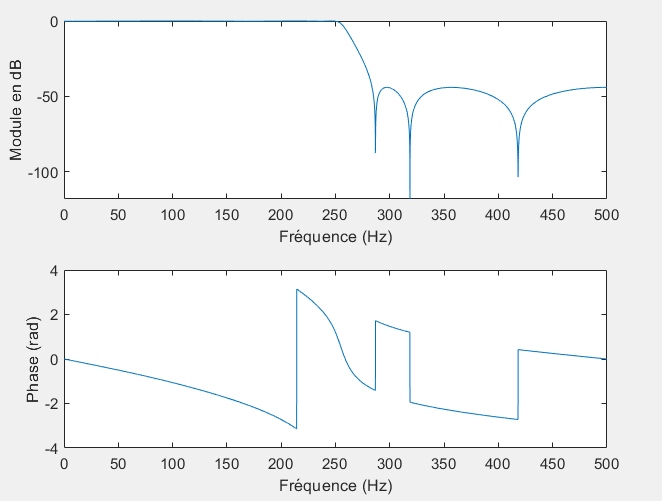
end4- Calculer le transformée de Fourier de la réponse impulsionnelle du filtre stable (revoir la question 1), et puis tracer son module en dB et sa phase.
B=[0.0725 0.2200 0.4085 0.4883 0.4085 0.2200 0.0725];
A=[1.0000 -0.5835 1.7021 -0.8477 0.8401 -0.2823 0.0924];
N = 10000; % Nombre d'échantillons
Ts = 1e-4; % Période d'échantillonage
% Réponse impulsionnelle du filtre
h = impz(B, A, N);
% Transformée de Fourier de la réponse impulsionnelle
H = fft(h);
% Fréquences correspondantes
f = linspace(0, 1/(2*Ts), N/2+1);
% Tracer le module en dB
subplot(2,1,1)
plot(f, 20*log10(abs(H(1:N/2+1))));
xlabel('Fréquence (Hz)');
ylabel('Module en dB');
% Tracer la phase
subplot(2,1,2)
plot(f, angle(H(1:N/2+1)));
xlabel('Fréquence (Hz)');
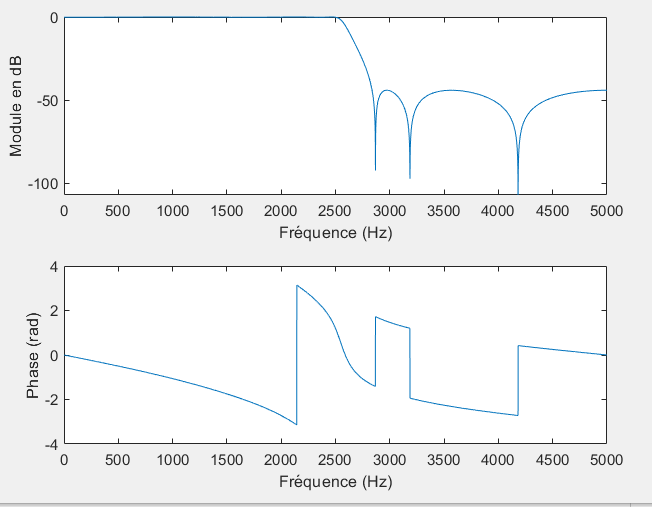
ylabel('Phase (rad)');5- Calculer la transmittance en Z de ce filtre sur le vecteur fréquences défini précédemment, en faisant appel à la fonction « transfert », et puis tracer son module en Db et sa phase. Comparer ce dernier avec celui obtenu dans la question précédente. Conclure.
[H,H_f,w] = transfert(B,A,N,te);
% Tracer le module en dB
subplot(2,1,1)
plot(w, 20*log10(abs(H_f)));
xlabel('Fréquence (Hz)');
ylabel('Module en dB');
% Tracer la phase
subplot(2,1,2)
plot(w, angle(H_f));
xlabel('Fréquence (Hz)');
ylabel('Phase (rad)');==> Pour conclure, on peut dire que la transmittance en Z est une bonne méthode pour étudier la réponse fréquentielle d'un filtre IIR, et que dans le cas d'un filtre stable, la transmittance en Z est très proche de la transformée de Fourier de la réponse impulsionnelle.
Fs = 1e4;
TS=1/Fs;
% bande passante et bande attenuante normalisées
Freq_Pass = 500/Fs;
Freq_Att =570/Fs;
Attenuation_Min=0.2;
% Atténuation minimale
Attenuation_Max=45;
%Attenuation maximale
N =100;
%Nombre choisi de coefficients du filtre
%Synthese du filtre
Filter= firpm(N-1, [0 Freq_Pass Freq_Att 1], [1 1 0 0], [Attenuation_Min Attenuation_Max]);
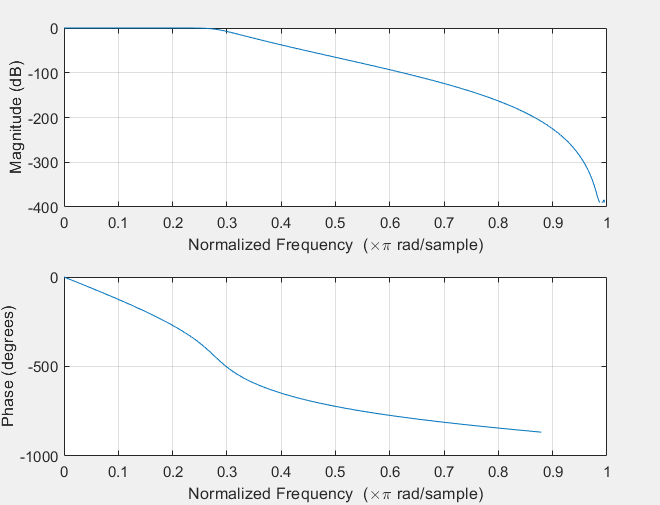
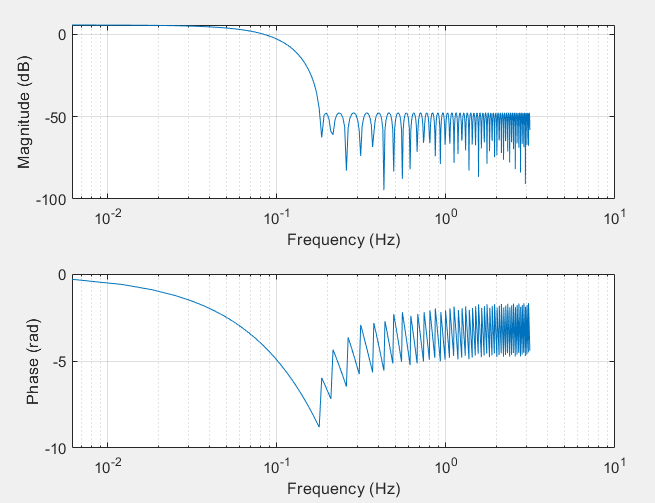
[H_Fun, ff]=freqz(Filter);subplot(2,1,1);
semilogx(ff,20*log10(abs(H_Fun)));
xlabel('Frequency (Hz)');
ylabel('Magnitude (dB)');
grid on
subplot(2,1,2);
semilogx(ff,unwrap(angle(H_Fun))); %"unwrap" est une fonction en MATLAB utilisée pour corriger les sauts d'phase d'un signal périodique.
xlabel('Frequency (Hz)');
ylabel('Phase (rad)');
grid on- Réaliser la conception d’un filtre FIR permettant de filtrer les deux signaux sonores traités dans la partie 1. Appliquer ce filtre.
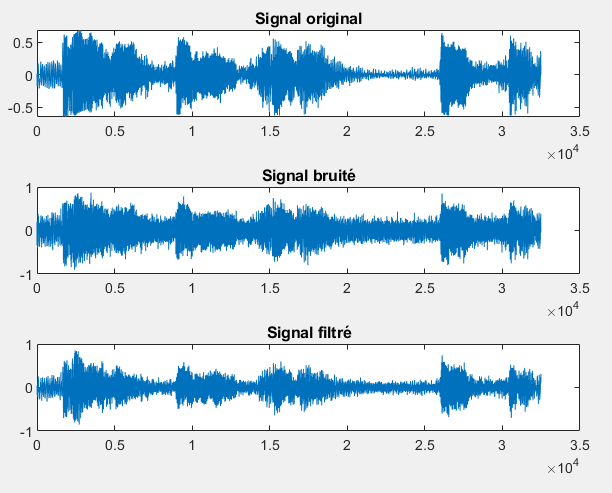
[signal1,fe]=audioread('affreux_bruite.wav');
akesuper_Filter_Order = 90;
akesuper_Cutoff_Freq = [0 Fc Fc*2 1];
akesuper_Cutoff_Gain = [1 1 0 0];
akesuper_Filter=firpm(akesuper_Filter_Order,akesuper_Cutoff_Freq,akesuper_Cutoff_Gain);
filtered_signal1 = filter(akesuper_Filter,1,signal1);Fc = 0.35; % fréquence de coupure en Hz
[signal2,fe2]=audioread('akesuper_bruite.wav');
affreux_Filter_Order = 90;
affreux_Cutoff_Freq = [0 Fc Fc*2 1];
affreux_Cutoff_Gain = [1 1 0 0];
affreux_Filter=firpm(affreux_Filter_Order,affreux_Cutoff_Freq,affreux_Cutoff_Gain);
filtered_signal2 = filter(affreux_Filter,1,signal2);