- Objectifs.
- Représentation temporelle et fréquentielle.
- Analyse fréquentielle du chant du rorqual bleu.
~Representation de signaux et applications de la transformee de Fourier discrete(TFD) sous Matlab
~Evaluation de l'interet du passage du domaine temporel au domaine frequentiel dans l'analyse et l'interpretation des signaux physiques reels
Il est à remarquer que ce TP traite en principe des signaux continus.Or, l'utilisation de Matlab suppose l'échantillonnage du signal. Il faudra donc être vigilant par rapport aux différences de traitement entre le temps continu et le temps discret.
toutes les figures devront être tracées avec les axes et les légendes des axes appropriés.
un script Matlab commenté contenant le travail réalisé et des commentaires sur ce que vous avez compris et pas compris, ou sur ce qui vous a semblé intéressant ou pas, bref tout commentaire pertinent sur le TP
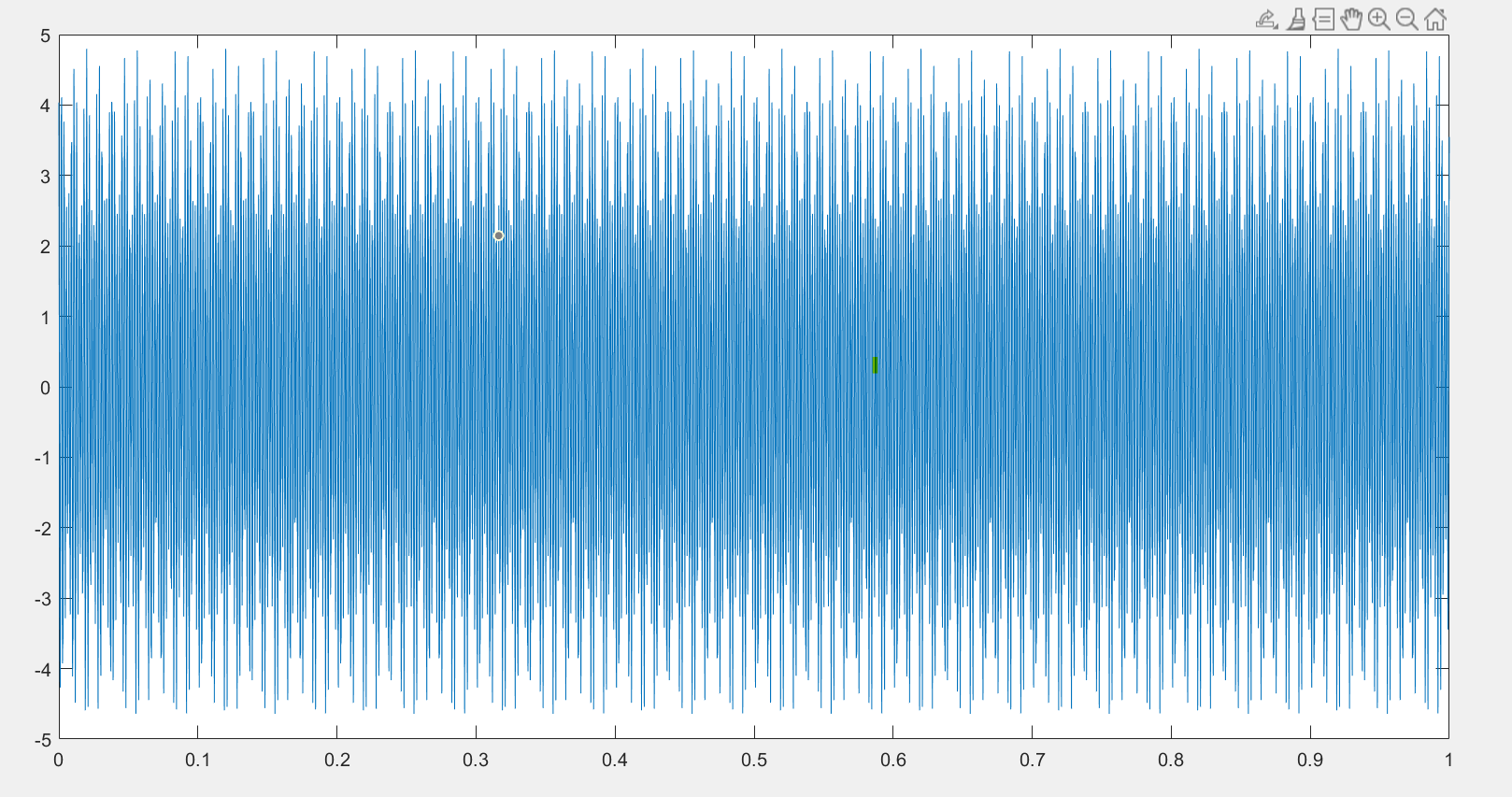
Considérons un signal périodique x(t) constitué d’une somme de trois sinusoïdes de fréquences 440Hz, 550Hz, 2500Hz.
1- Tracer le signal x(t). Fréquence d’échantillonnage : fe = 10000Hz, Intervalle : Nombre d’échantillons : N = 5000.
fe = 1e4; % frequence d echantillonnage
te = 1/fe; % pas d echantillonnage
N = 10000; % nombre d echantillons (points)
t = (0:N-1)*te; % intervalle de temps
x = 1.2*cos(2*pi*440*t+1.2)+3*cos(2*pi*550*t)+0.6*cos(2*pi*2500*t);
plot(t,x,'.');
title('signal x(t) :');
Pour approximer la TF continue d’un signal x(t), représenté suivant un pas Te, on utilise les deux commandes : fft et fftshift.
• On remarquera que la TF est une fonction complexe et que la fonction ainsi obtenue décrit la TF de x(t) entre –1/(2Te) et 1/(2Te) par pas de 1/(nTe) où n est le nombre de points constituant le signal x(t).
• La commande fft codant les fréquences positives sur les n/2 premières valeurs du signal et les valeurs négatives entre n/2+1 et n, la commande fftshift permet de les inverser.
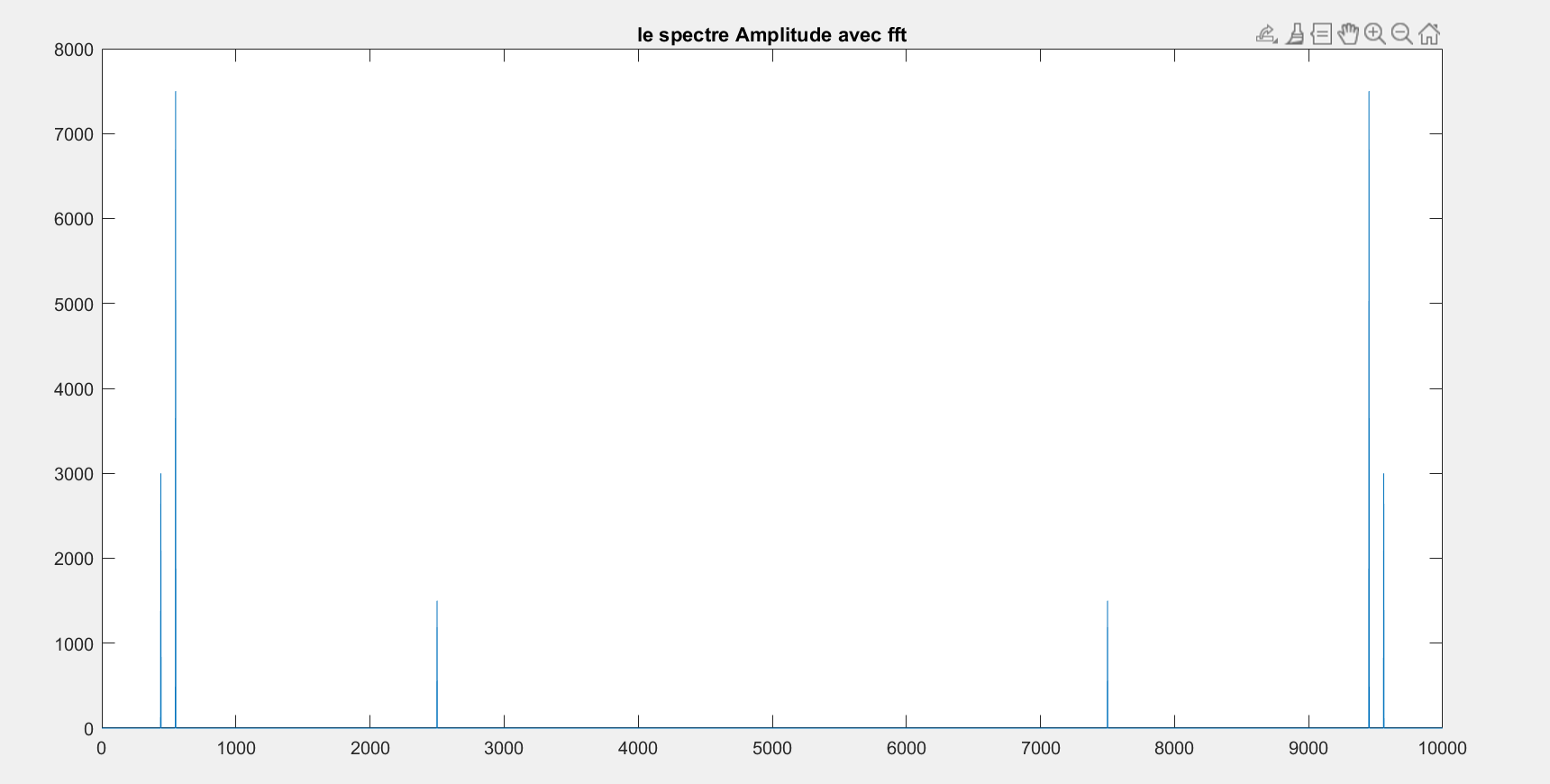
2- Calculer la TFD du signal x(t) en utilisant la commande fft, puis tracer son spectre en amplitude après avoir créé le vecteur f qui correspond à l'échantillonnage du signal dans l'espace fréquentiel. Utiliser la commande abs pour afficher le spectre d’amplitude.
f =(0:N-1)*(fe/N); %frequence du spectre
y = fft(x); % y: spectre , fft(x) : transformee de fourier
plot(f,abs(y));
title('le spectre Amplitude avec fft');
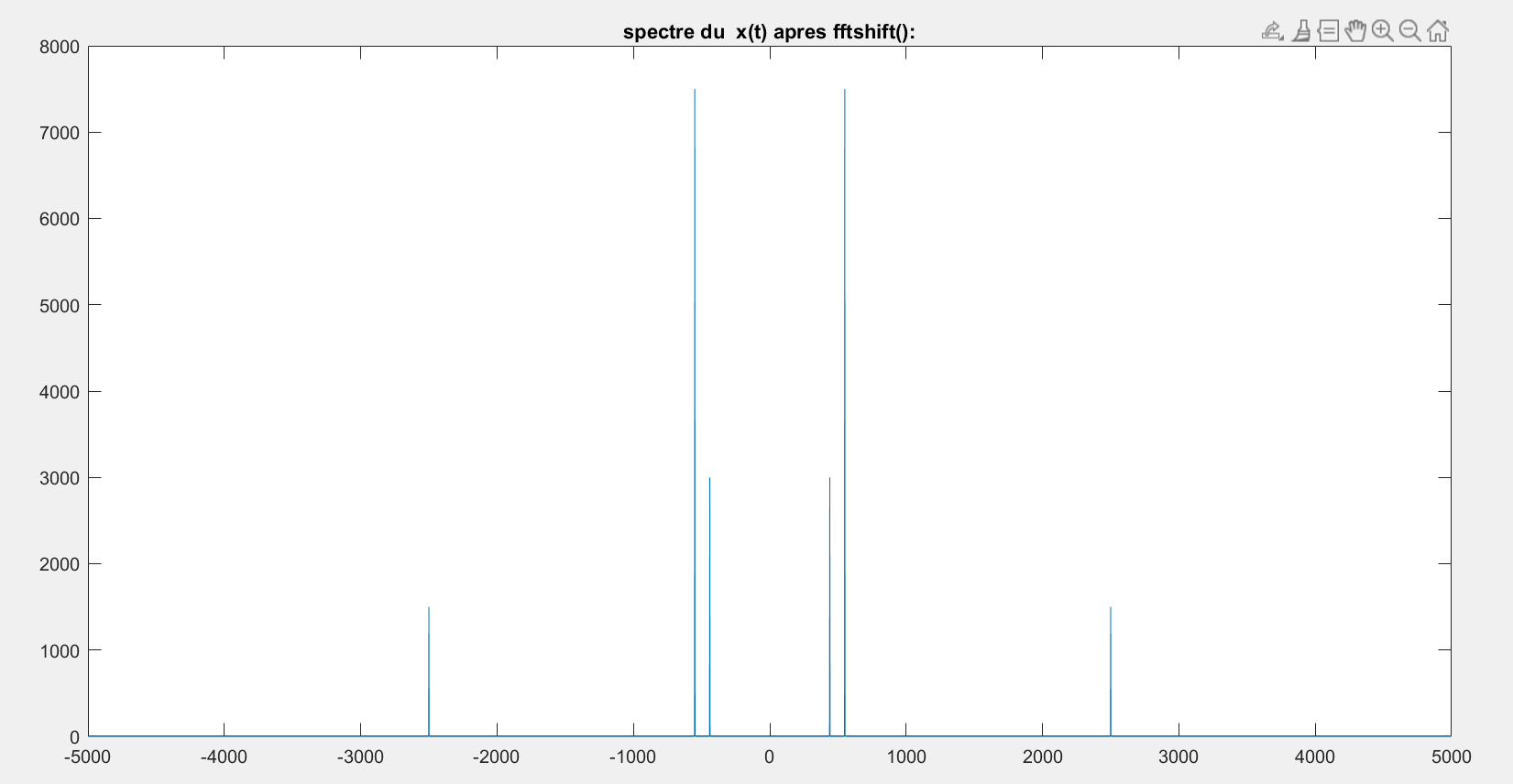
3. Pour mieux visualiser le contenu fréquentiel du signal, utiliser la fonction fftshift, que effectue un décalage circulaire centré sur zéro du spectre en amplitude obtenu par la commande fft
fshift = (-N/2:N/2-1)*(fe/N);
plot(fshift,fftshift(abs(y)));
title('spectre du x(t) apres fftshift():');
Un bruit correspond à tout phénomène perturbateur gênant la transmission ou l'interprétation d'un signal. Dans les applications scientifiques, les signaux sont souvent corrompus par du bruit aléatoire, modifiant ainsi leurs composantes fréquentielles. La TFD peut traiter le bruit aléatoire et révéler les fréquences qui y correspond
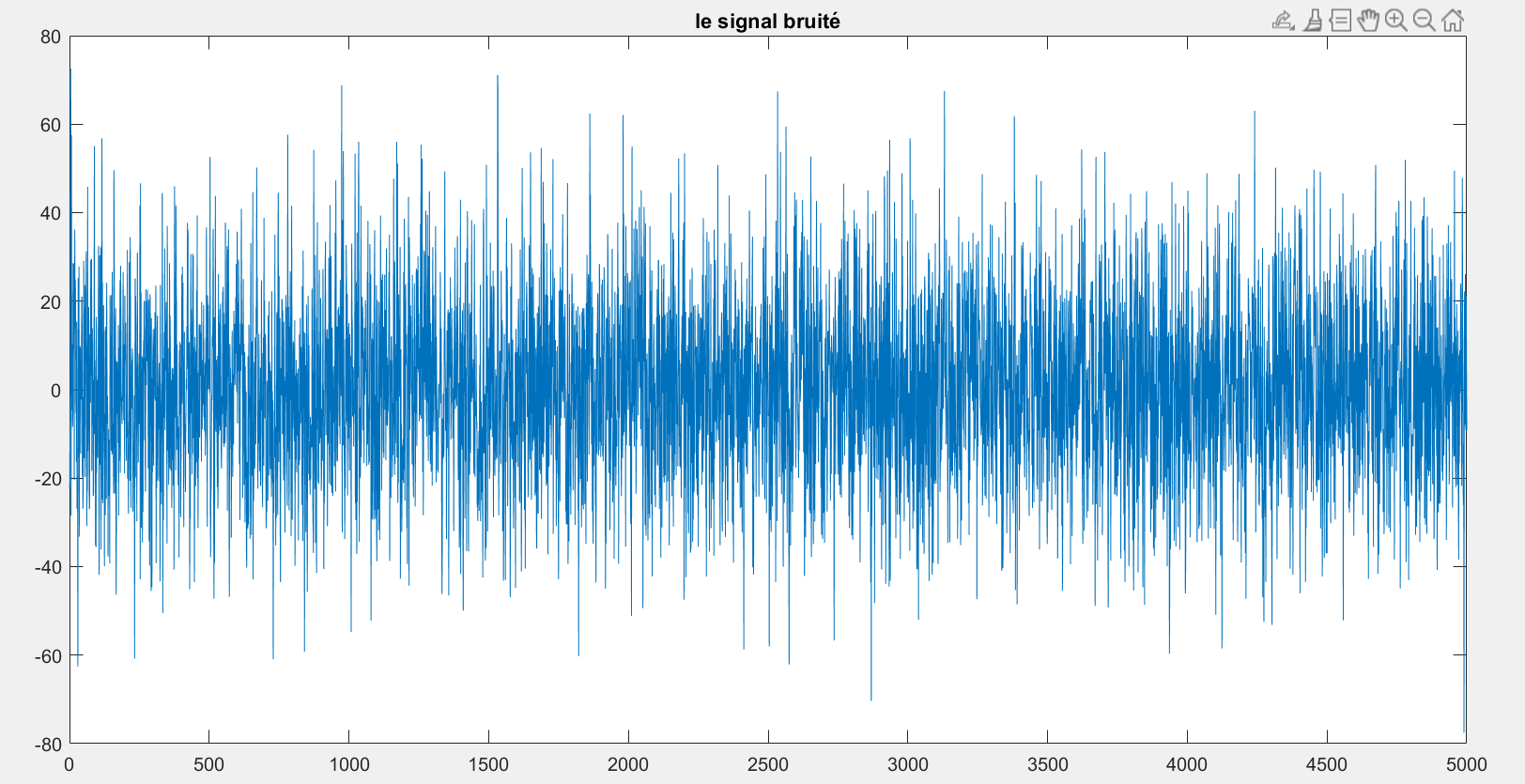
4- Créer un nouveau signal xnoise, en introduisant un bruit blanc gaussien dans le signal d’origine x(t), puis visualisez-le. Utiliser la commande randn pour générer ce bruit. Il est à noter qu’un bruit blanc est une réalisation d'un processus aléatoire dans lequel la densité spectrale de puissance est la même pour toutes les fréquences de la bande passante. Ce bruit suit une loi normale de moyenne 0 et d’écart type 1
bruit = 20*randn(size(x));%bruit
xnoise = x+bruit; % signal+bruit
plot(xnoise);
title('le signal bruité') sound(x) %le signal
sound(xnoise) %le signal bruité
La puissance du signal en fonction de la fréquence (densité spectrale de puissance) est une métrique couramment utilisée en traitement du signal. Elle est définie comme étant le carré du module de la TFD, divisée par le nombre d'échantillons de fréquence
xnoise = x+bruit; % signal+bruit
fshift = (-N/2:N/2-1)*(fe/N);
ybruit = fft(xnoise);
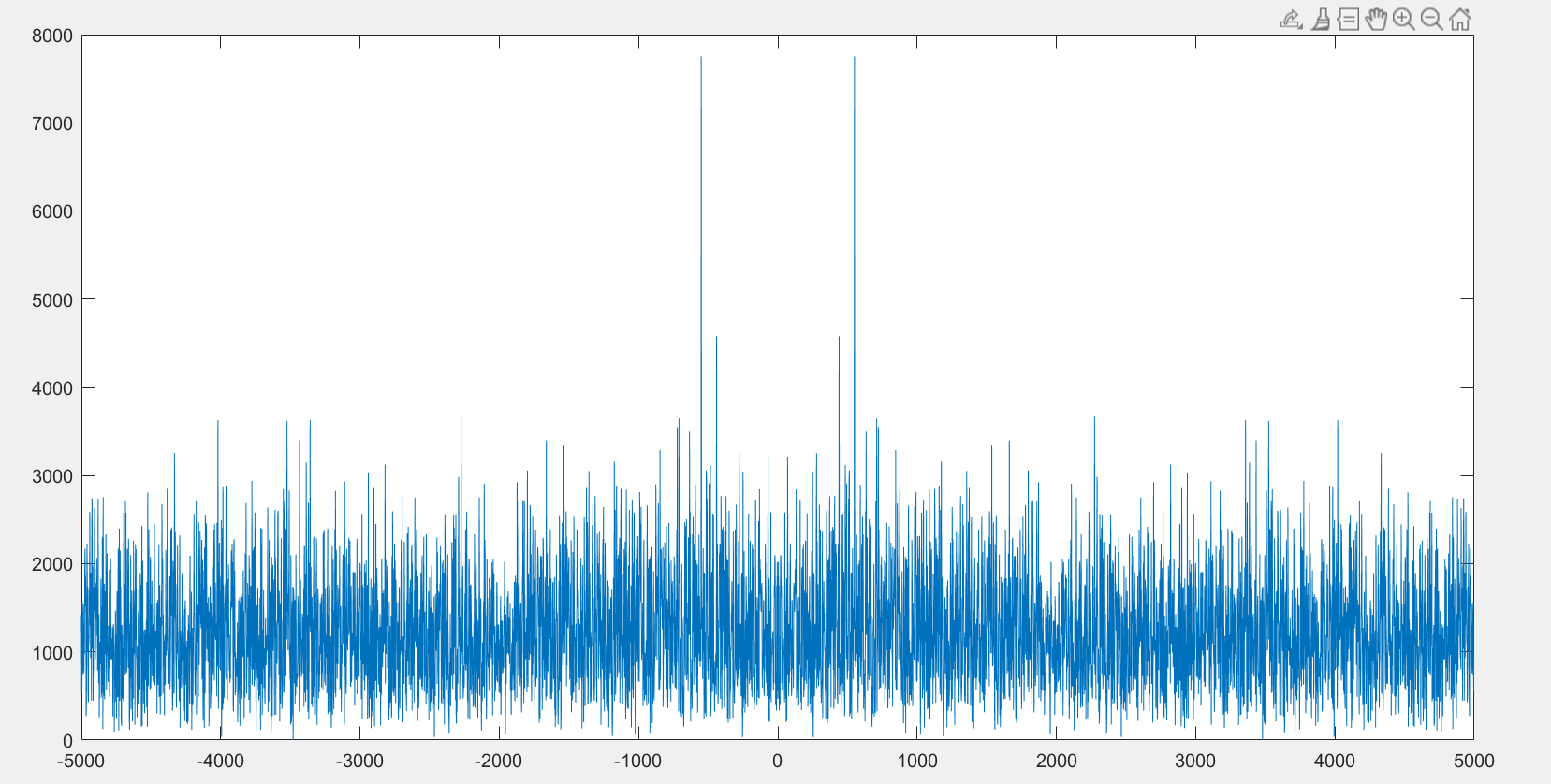
plot(fshift,fftshift(abs(ybruit)));
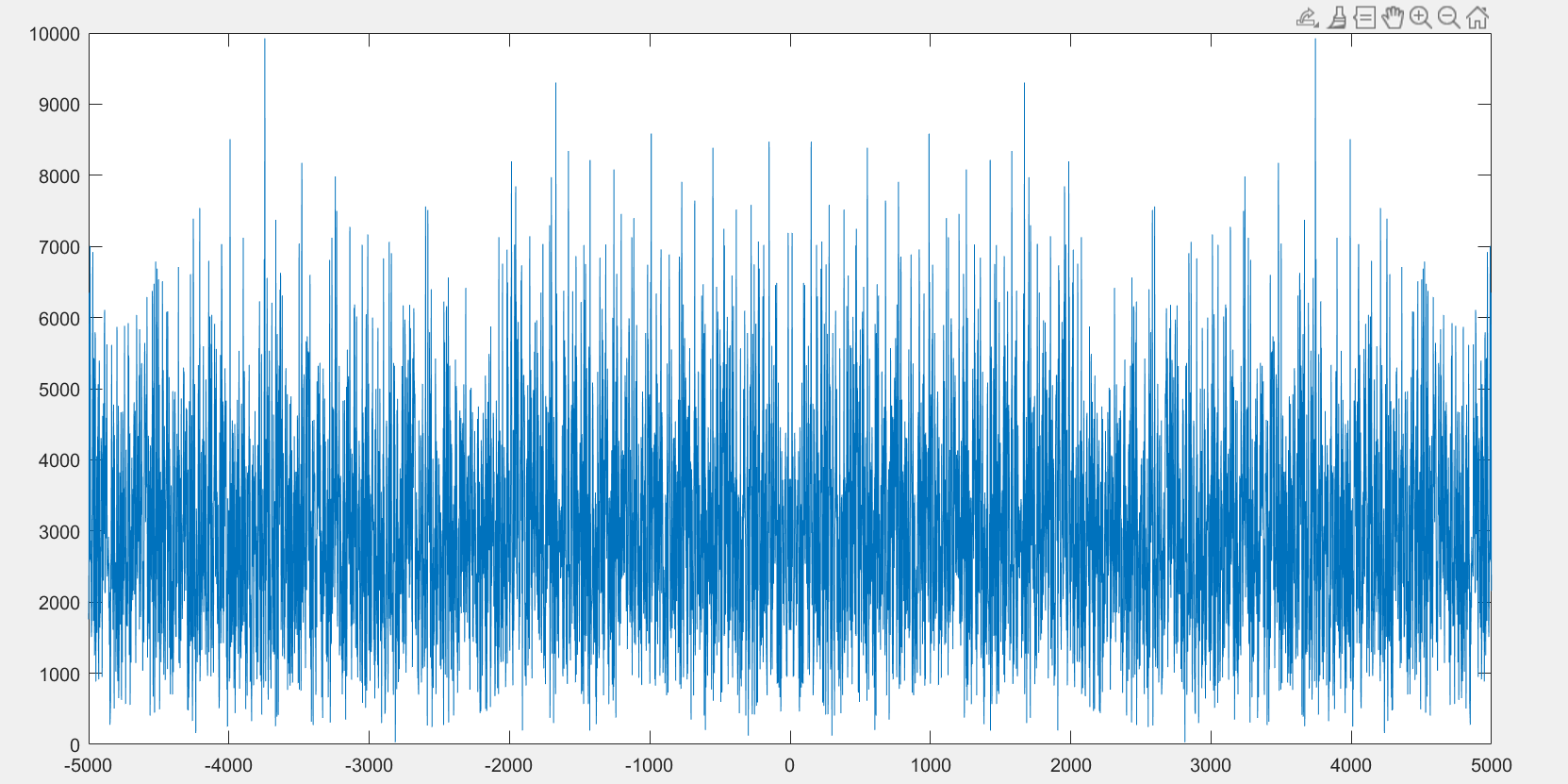
bruit = 50*randn(size(x));%bruit
xnoise = x+bruit; % signal+bruit
fshift = (-N/2:N/2-1)*(fe/N);
ybruit = fft(xnoise);
plot(fshift,fftshift(abs(ybruit)));lorsqu'on augmente l’intensité de bruit, on perd le signal informative
Il existe plusieurs signaux dont l’information est encodée dans des sinusoïdes. Les ondes sonores est un bon exemple. Considérons maintenant des données audios collectées à partir de microphones sous - marins au large de la Californie. On cherche à détecter à travers une analyse de Fourier le contenu fréquentiel d’une onde sonore émise pas un rorqual bleu.
1- Chargez, depuis le fichier ‘bluewhale.au’, le sous-ensemble de données qui correspond au chant du rorqual bleu du Pacifique. En effet, les appels de rorqual bleu sont des sons à basse fréquence, ils sont à peine audibles pour les humains. Utiliser la commande audioread pour lire le fichier. Le son à récupérer correspond aux indices allant de 2.45e4 à 3.10e4
[x,fs] = audioread("bluewhale.au");
chant = x(2.45e4:3.10e4);sound(x,fs)
chant = x(2.45e4:3.10e4);
N=length(chant);
ts=1/fs;
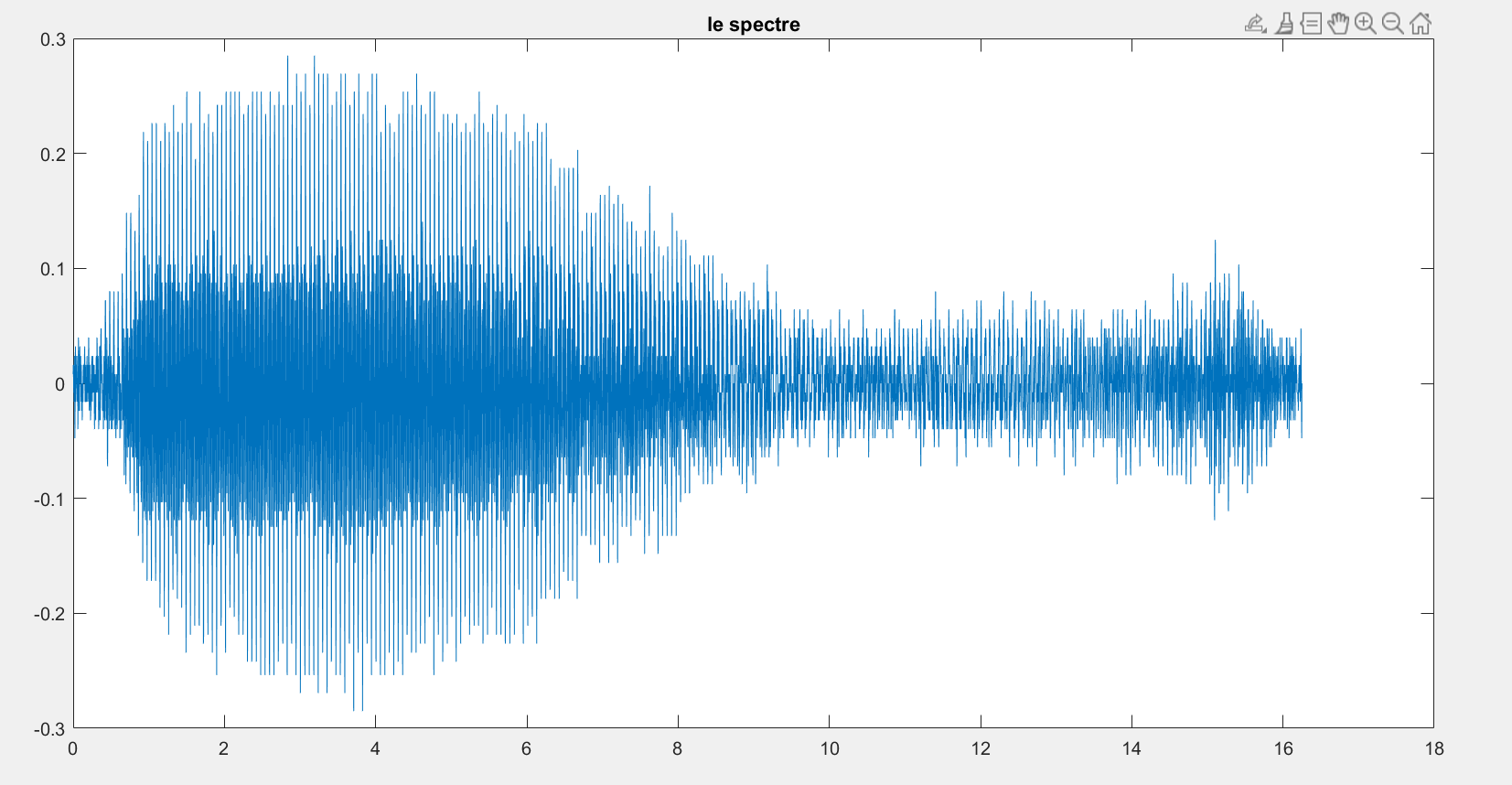
t=(0:N-1)*(10*ts);
plot(t,chant);La TFD peut être utilisée pour identifier les composantes fréquentielles de ce signal audio. Dans certaines applications qui traitent de grandes quantités de données avec fft, il est courant de redimensionner l'entrée de sorte que le nombre d'échantillons soit une puissance de 2. fft remplit automatiquement les données avec des zéros pour augmenter la taille de l'échantillon. Cela peut accélérer considérablement le calcul de la transformation
3- Spécifiez une nouvelle longueur de signal qui sera une puissance de 2, puis tracer la densité spectrale de puissance du signal
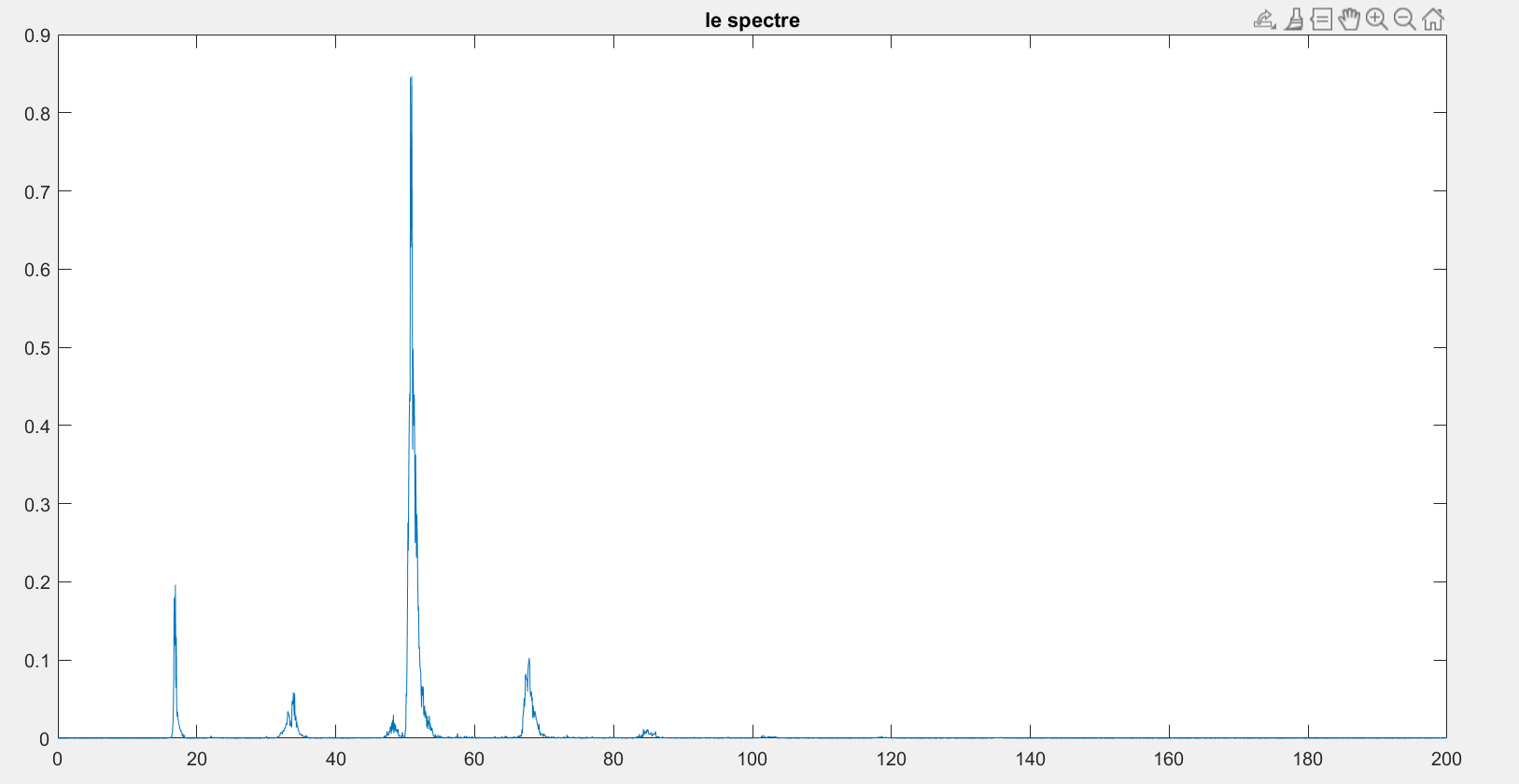
dsp_chant = (abs(fft(chant)).^2)/N;
f = (0:floor(N/2))*(fs/N)/10;
plot(f,dsp_chant(1:floor(N/2)+1))
title('le spectre')c'est la fréquence de premier pic qui est entre 16Hz-17Hz (16.92)