This repository contains the implementation of a general formula for calculating hyperplane sums in a Pascal Simplex.
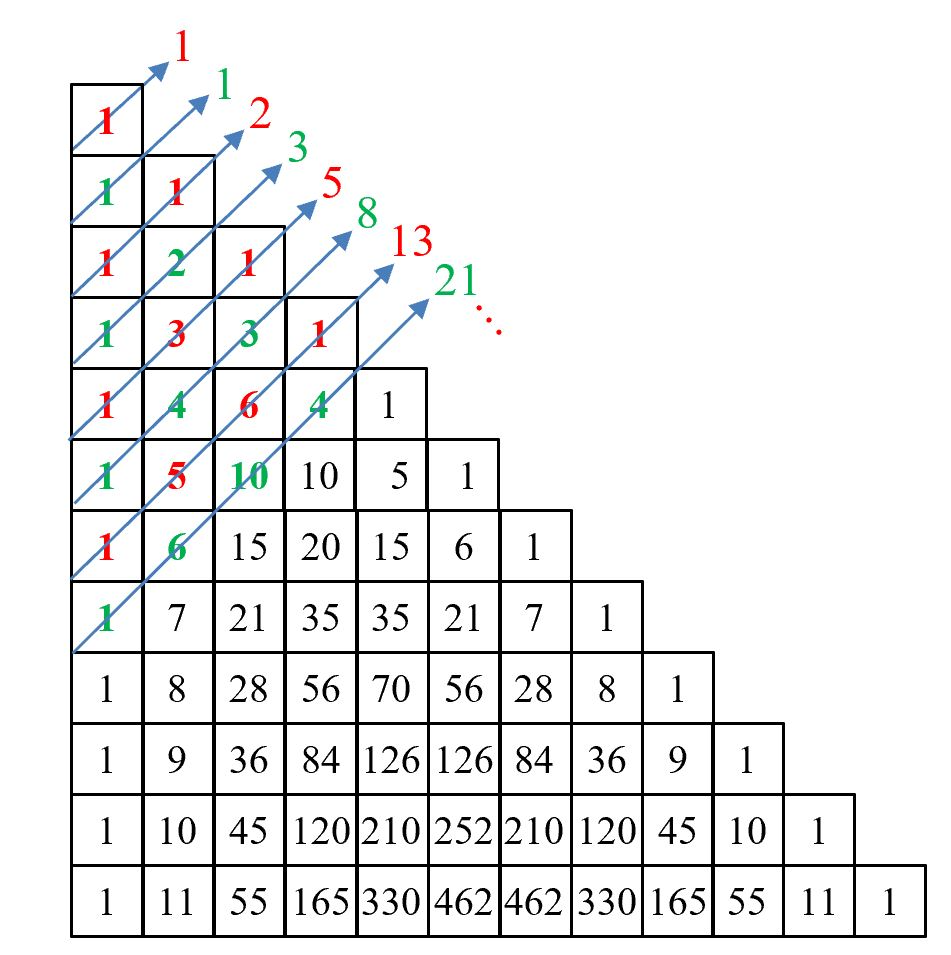
Pascal’s Triangle is one of the most fascinating mathematical structures, appearing in numerous areas of mathematics, from combinatorics to number theory. It is built by arranging binomial coefficients in a triangular pattern, revealing surprising relationships between numbers. One such connection, perhaps lesser known, links Pascal’s Triangle to the Fibonacci sequence.
The Fibonacci sequence is a simple yet powerful sequence of numbers, where each term is the sum of the two preceding ones. It appears in nature, art, and even financial models. Remarkably, hidden within Pascal’s Triangle, Fibonacci numbers can be discovered along specific diagonal paths, as you can see in the picture below.
As you can see, the sequence of diagonal sums equals the Fibonacci sequence, which is defined as:
In this notebook, we will explore this connection in greater depth and extend it beyond two dimensions. By generalizing Pascal’s Triangle into higher-dimensional structures, known as Pascal simplices, we will uncover a formula for summing elements along specific hyperplanes. This exploration will not only deepen our understanding of Pascal’s Triangle and the Fibonacci sequence but also reveal elegant mathematical patterns that emerge in higher dimensions.