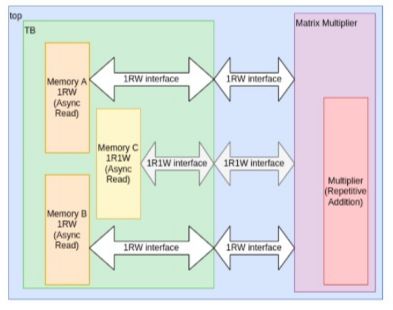
Takes two 10x10 matrices stored in two different 1rw memories and calculate result through repetitive addition and store resultant matrix C back in 1r1w memory.
Underlying working of proposed algorithm is same as we typically multiply two matrices i.e, we take first row of matrix A and first column of matrix B, multiply them element by element and then add their product repetitively and we get first element of matrix C (resultant matrix), and repeat this process for all rows and columns (You can find complete detail here https://en.wikipedia.org/wiki/Matrix_multiplication).
We can’t directly apply above provided algorithm in our case because in our case we have matrices stored in memories and resultant is also going to be stored in memory so in addition to doing multiplication and addition of elements, we also need to generate addresses for three different memories to load and store our data into these memories.
Matrices A and B both are stored in memories in a continuous row wise position i.e, from address 0-9 first row is stored, from address 10-19 second row is stored and so on.
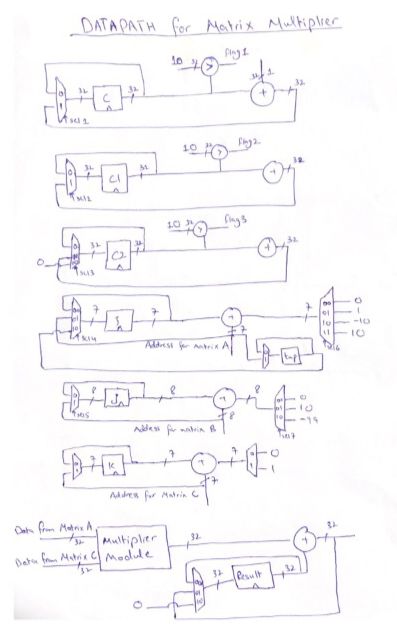
Hence in order to generate addresses for these three different memories, we used three counters, and these counters are continuously incrementing with value of 1 in case of accessing/storing elements of/to row and incrementing with value of 10 in case of accessing elements of column. And of course there are some flags which are controlling when to increment these counters.
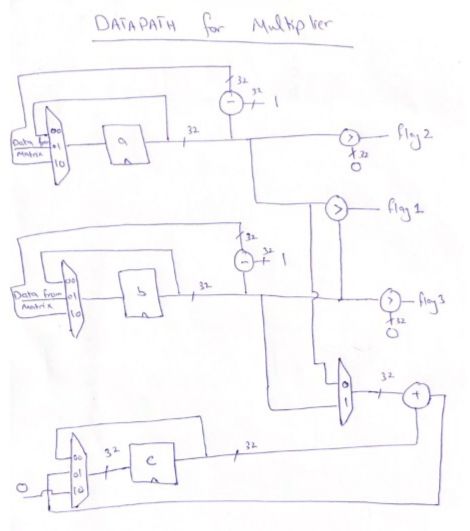
We divided our Matrix Multiplier into two parts i.e, one part is a multiplier fsm which is multiplying two values by repetitive addition and second part is matrix multiplier fsm which is generating addresses and doing summation of products of different element (output of multiplier fsm) and storing it into resultant matrix.
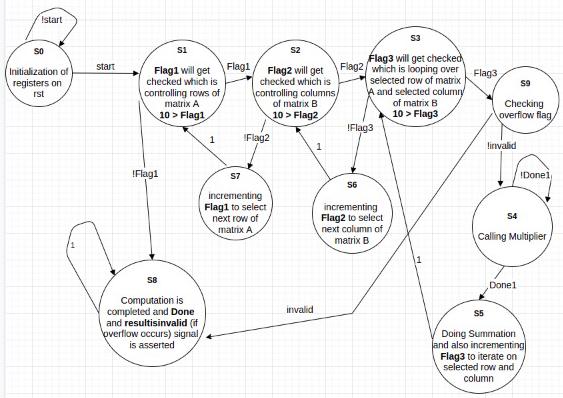
State diagram of multiplier’s fsm is given as below:
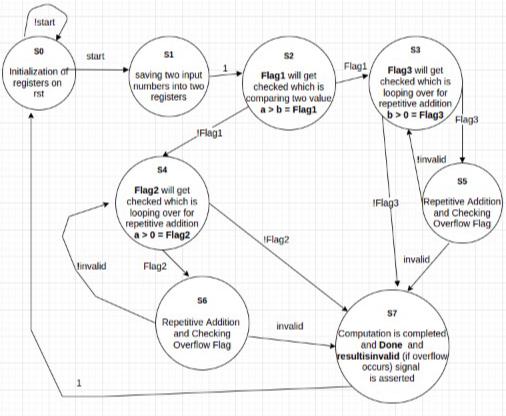
The State Diagram of matrix multiplier’s fsm is given as below:
The above provided State Diagrams of multiplier and matrix multiplier implements moore state machines. The reason to go with the moore state machine is that with moore we can have more control on our outputs and state transitions i.e, as output depends only upon current state and as state transition is synchronous so everything is happening synchronously.
Block diagram for multiplier fsm is given as below:
Datapath for Matrix Multiplier fsm is given as below: