Blender: Lead Edge Ash Extension

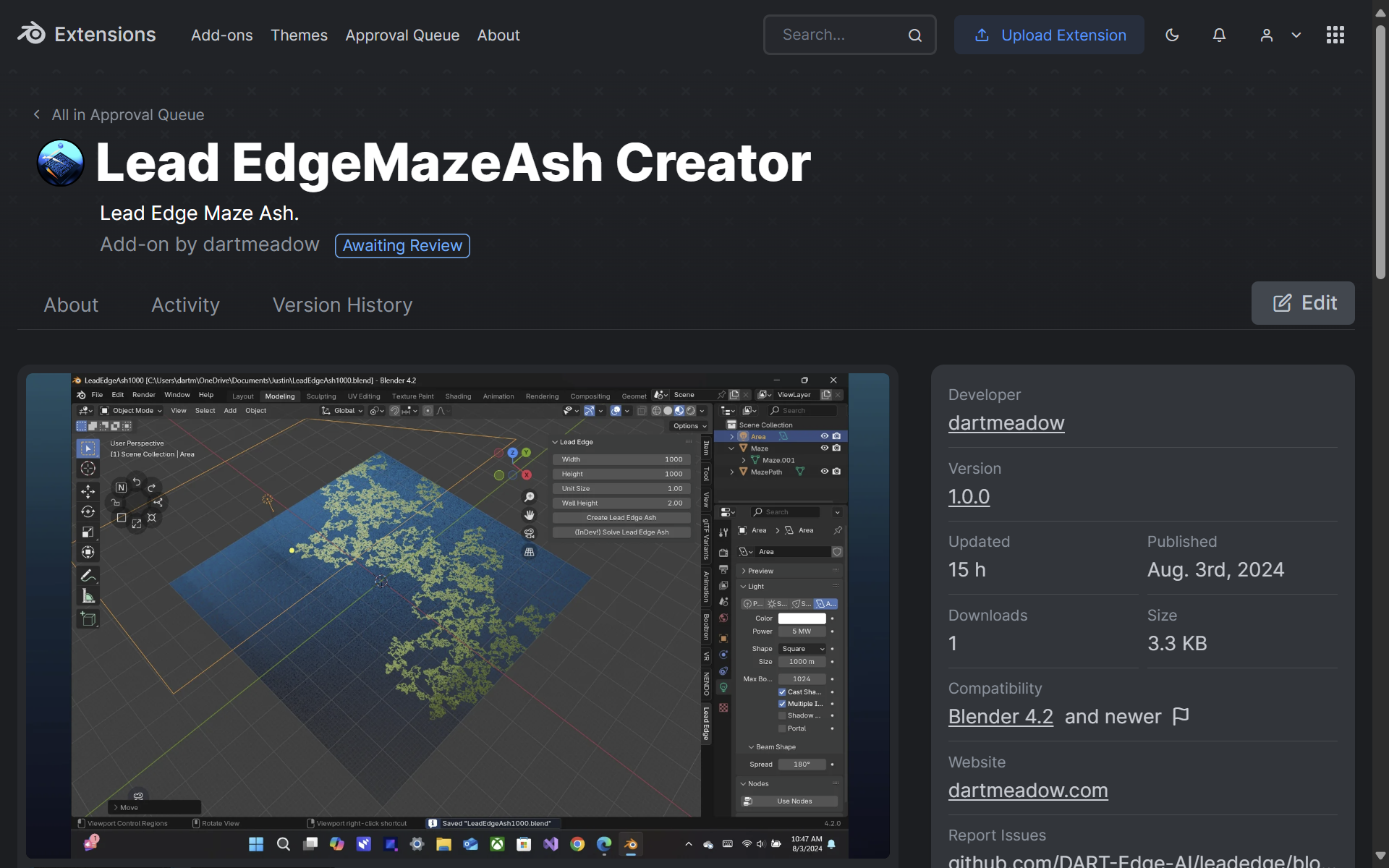
Available on Blender Extensions: Lead Edge Maze Ash Creator

Usage:

1. Open the Properties Pane: Shorcut "N"

2. Access the Lead Edge Panel

3. Specify Deminsions

4. Generate Lead Edge Ash

5. Optional: Solve Lead Edge Ash

Have a support inquiry? Contact us with this: Support Form

Currently The Path is Solvable but the 2 perimeter openings are not Marked. You May select 2 segements along the Path Mesh ends where the Path Mesh meets the Perimeter to edit your own openings or for larger Iterations anywhere along the Path Mesh where the Path Mesh meets the perimeter to speed up the Project Flow.

Add-on Install from zip: Lead Edge

1. Blender: Preferences
2. Add-ons tab
3. Upper right Corner Menu Popup: Install From Disk, Select Downloaded Zip
4. Enable and Save Preferences then Blender Startup File

Direct blender Script import/copy/paste in lender script editor - press play. download: Lead Edge

Lead Edge Algorithm for Ash Tree Reflex Autumn's Root Algorithm

Author: Justin Craig Venable LeadEdge - (Maze Pathfinding Algorithm) Section 1:

Path Solved (Axis x and y vector line rules):

D3.e= (D3.f=(D3=((((((b+b)(a^2))/2)=(r+1)/2)-(((b+b)(a^2))/2)=r)=(D1+D2))))

D3.f=(D3=((((((b+b)(a^2))/2)=(r+1)/2)-(((b+b)(a^2))/2)=r)=(D1+D2)))

D3=((((((b+b)(a^2))/2)=(r+1)/2)-(((b+b)(a^2))/2)=r)=(D1+D2))

D3.e = is iterated from center canvas pixel at top, right, bottom and left with a random of operation itself against itself in the top,right,bottom and left directions at the same time to the nearest direction on math completion to pick the first direction is counterclockwise is iterated initially then clockwise second. Upon this iteration complete the same iteration picks up operation at the result to determine the nearest corner pixel to begin line draw.

The core formula (b+b)(a^2)=0 acts as a random placeholder counter for d3.e to pick the first opening position randomly on the maze perimeter then the sub formulas flow from there, but for the second generation and every after to always be randomly different the core logic adds a unit to itself for each generation in the core logic counter placeholder Generation 1: (b+b)(a^2)=0, Generation 2: ((b+b)(a^2))+1n=2n, Generation 3: ((b+b)(a^2))+1n=3n to desired finite Generations.

In elementary terminology for computer programming (b+(b+1))*(a^2) will show that the same subject of variable b is the 2 maze perimeter walls, the first position and the second in a different position increase of 1 to the first perimeter and canvas. This will allow each perimeter to watch out from running into the other perimeter during complete canvas propagation for every generation.

The goal is to actually use the Lead Edge Algorithm as is during creation and for result therefore any code logic used is only a plus 1 inrecrement from last starting position such as the the canvas center or size that forces the Lead Edge formula to daisy chain the remaining formula providing a natural finite measuring biproduct tool to build a different new generation than the previous. This allows a Lead Edge Maze to be only math generated and not dependent on other natural finite logic makers such as physics or computer time, time stamps, degrees, radians - (which is the state of a subject, are you on your lawn in the sun today or in the rain today?, same subject and habitat but the habitat may be different, one day a gas versus the next a liquid). We want to reserve the variables for the fun in Lead Edge by its purpose for use in real world Research and Development as well as Industrial Production, connecting to outside sources, data and hardware.

D3.f = nearest corner pixel to begin draw

“a” is the square foundation, perimeter, viewport or canvas

“b” is the foundation for wall and path dimensions which should be equal but can be random.

D1 is Division 1

D2 is Division 2

R will serve as the pathfinding function to both points "a" and "b".

a = Begin b = Destination

r must find the shortest path to b or in reverse to a. do not path find in reverse unless explicitly specified.

r will design the infrastructure with vector lines to both halves of the maze. Lines will be constructed at random lengths and angles but never intersect and never leave other lines in a loop to itself within the maze field perimeter. Mazes will be constructed for a goal to reach a different side than beginning or reach a single destination within the maze field perimeter or a goal of leaving the designated begin within the maze field perimeter to a single exit point Destination.

Design the maze with r using these rules.

If division 2 math perfectly loops then division 1 can abide by the 5px and 2px to randomly generate the lines:

Create a toolbar to specify maze dimensions on two axis, x and y, with a generate button.

Have the maze generated as white above the html page.

Section 2:

LeadEdge Function Divisions:

Division 1 (Wall Generation): D1 runs the algorithm in two primary instances for which are wall one then wall two looking inwards on the current wall being generated while leaving two openings on the perimeter.

Sw: Sub Wall Sw^n: SubWall to the nth

Wall 1 : Sub iteration for random seeding branches that have their own random turns with segments which are a completely new wall attached to the main Wall 1 ((Sw)(((b+b)(a^2))). Each branch off the main wall can have their own random sub branches ((Sw^n)(((b+b)(a^2))) until the main wall's propagation fills between the openings of the perimeter within the mazeSize.

Wall 2 : Sub iteration for random seeding branches that have their own random turns with segments which are a completely new wall attached to the main Wall 2 ((Sw)(((b+b)(a^2))). Each branch off the main wall can have their own random sub branches ((Sw^n)(((b+b)(a^2))) until the main wall's propagation is filled between the openings of the perimeter within the mazeSize.

The Following LeadEdge Math Algorithm must Randomly draw webgl cell geometry of no more than 1 cell unit apart from each branch iteration and no closer than one cell unit of empty space then have at random only 90 degree turns for each random generation Iteration segments.

D1 Main Iteration: (((b+b)(a^2)) D1 Branch Iteration: ((Sw)(((b+b)(a^2))) D1 Sub Branch Iteration ((Sw^n)(((b+b)*(a^2)))

D1= [(((b+b)(a^2))/2)=(r+1)/2 which is the sigma of two iterations: D1 first b iteration [wall 1: (((b+b)(a^2))], [D1 second iteration [wall 2: (((b+b)*(a^2))]]

Division 2 (Path Finding core math): D2 is a redundancy checker against D1 where D1 iterations look inwards to build the walls, D2 uses those iterations to look outward from the path much like an inverse logic operation verifying D1 is performing generations correctly.

If wall line dimensions are specified in Division 1 then the path finding Math must abide by Division 1 as well the entrance and exit dimensions therefore “r” must be continuously compared to Division 1 and 2 to fully generate the maze with the following math positioned between the walls that is part of Division 1 :

[D2 The Path: (Sw)+(Sw^n)+(((b+b)*(a^2))/2)=r] Where divided by two is both D1 wall iterations and r is the proportional path.

D1 first b iteration [wall 1: (((b+b)(a^2))] D1 second iteration [wall 2: (((b+b)(a^2))] Then Branch Iterations: (Sw) and Sub Branch Iterations: (Sw^n)

Section 3:

Where (D1+D2) is path finding Then:

Division 3 (Axis of x and y abide by Section 1 D3): D3 is primarily an accessor function for external code, AI and hardware access.

function D3: d3function1[((((((b+b)(a^2))/2)=(r+1)/2)] - d3function2[(((b+b)(a^2))/2)=r)] = D1 + D2

Such that function D3 iterates in d3function1 while subtracting the completed maze in d3function2

The extra iteration in function D3 result is held constant to perform checks and recursive validating function D1 and D2 during build.

function D3: (by reference: allocates an open variable with capable of iterations like: an^2√an=b)

R of d1 and d2 Finally must continuously compare to (D1+D2) to fully generate the maze.

“r” of D1 andD2 is line and path plot, (D1+D2) is the path Solved.

D1 is iterated over each rand decision of line length and 90 degree turns:

D2 is iterated in comparison to D1 for “build solve” between the lines, the path.

D3 is the solved iteration.

D3.e is begin decision.

D3.f is begin draw.

The core math of (Sw)+(Sw^n)+(((b+b)*(a^2))/2)=r should alone solve a destination between two points. So to implement this Full context with a functioning 2D html vector maze the Math rules are again implemented for html code rules to operate and build the code.

The core math loops so we are assigning the LeadEdge algorithm to perform at different starting intervals in D3.e and locations in D3.f therefore generation and solvability is simultaneously Functional.

Random Iteration Calibration (to aid the Lead Edge Algorithm in maintaining proportionality during random iteration):

Section 4:

Vector Calibration Code:

{"r=": " {"row1": "2+2", "column": "unspecified","row2": "2+2"} {"row3": "2+2", "column": "unspecified","row4": "2+2"} {"row5": "2+2", "center": "row1,2,3,4"} {"row6": "2-2", "column": "unspecified","row": "2-2", "rotation": "45:row1,2,3,4,5"} {"row7": "2-2", "column": "unspecified","row": "2-2", "rotation": "90:row6"} {"row8": "2+2", "center": "row9,10,11,12"} {"row9": "2+2", "column": "unspecified","row10": "2+2"} {"row11": "2+2", "column": "unspecified","row12": "2+2"}", "When r calculates: (((b+b)*(a^2))/2)=r"}

Elementary Steps for constructing the Maze:

STEP 1: Two geometry walls only with the D1 Function Iteration. The first wall starts in one direction building a solid perimeter but leaving Two openings - no more and no less than two openings. The second wall starts the opposite direction away from the first opening building a solid perimeter then both walls turn inwards to the mazeSize and propagate random turns and branches that can spawn off a wall cell side at random as long as the branches are no more than one wall thickness apart and no less than one wall apart. The random turn must be on the last wall segment cell side chosen at random and must continue straight at least one wall thickness before the wall can randomly turn again. Then Walls and their branches may never touch each other as well not touch each other at the cell corners, as in two corners that end after generation must be one wall thickness apart to provide path space. Maintain consistency with section D1: D1 Main Iteration: (((b+b)(a^2)), D1 Branch Iteration: ((Sw)(((b+b)(a^2))), D1 Sub Branch Iteration ((Sw^n)(((b+b)*(a^2))).

STEP 2: The solvable path must weave between the two walls from one opening to the other opening. The path space must be no more than one wall thickness and no less than one wall thickness. Dead ends may occur where branches don't form part of the main path between the two walls when the D1 function iterates the walls filling the mazeSize.

STEP 3: The Code may use no other maze generation or path finding algorithm except the Rules and Math found in these Lead Edge Algorithm Rules of this document.

STEP 4: There may only be no more and no less than one solvable path between the perimeter openings.

Elementary Random Iterations Steps:

Main Wall 1 (color: mediumvioletred): Must randomly start on the mazeSize perimeter and fill the perimeter with 1 unit thick geometry solid leaving an opening of space that is non geometry and 1 unit thick behind the direction the wall started then randomly stop providing the second opening space that is non geometry of 1 unit thick along the mazeSize perimeter then the wall1 will turn inwards to the maze size and randomly iterate turns every other 1 unit while randomly seeding new wall branches every other 1 unit which are independent SubWalls attached to the main wall1 with their own independent random turn iterations every other 1 unit and sub branches of the sub branches that are their own independent walls attached to the main sub branch as well their own turn iterations ever other 1 unit. The main wall1 and any sub branch system will propagate the maze size until it is filled for their half of the perimeter openings. The main wall1 and any sub branch system may never touch one another or meet next to each other at the cell sides and cell corners. The cell sides of the complete main wall1 system must always maintain a distance of 1 unit that is non geometry space as well the corners must maintain a 1 unit distance of non geometry space.

Main Wall 2 (color: deepskyblue): Must randomly start on the mazeSize perimeter and fill the perimeter with 1 unit thick geometry solid leaving an opening of space that is non geometry and 1 unit thick behind the direction the wall started then randomly stop providing the second opening space that is non geometry of 1 unit thick along the mazeSize perimeter then the wall2 will turn inwards to the maze size and randomly iterate turns every other 1 unit while randomly seeding new wall branches every other 1 unit which are independent SubWalls attached to the main wall1 with their own independent random turn iterations every other 1 unit and sub branches of the sub branches that are their own independent walls attached to the main sub branch as well their own turn iterations ever other 1 unit. The main wall2 and any sub branch system will propagate the maze size until it is filled for their half of the perimeter openings. The main wall2 and any sub branch system may never touch one another or meet next to each other at the cell sides and cell corners. The cell sides of the complete main wall2 system must always maintain a distance of 1 unit that is non geometry space as well the corners must maintain a 1 unit distance of non geometry space.

mazeSize: The two main wall systems must start opposite directions on the perimeter of the mazeSize next to the first opening then maintain a 1 unit non geometry space between the two walls at their cell sides and corners within the mazeSize perimeter. This complete 1 unit non geometry space path will provide a path space weaving between the two openings and main wall systems of no more than one solvable path and non less than one solvable path.

Elementary Core Math Definitions:

The core math: [(Sw)+(Sw^n)+(((b+b)*(a^2))/2)=r]: Used across all functions that construct the mazeSize perimeter main walls systems. The math is primarily there and all Lead Edge Algorithm Rules to validate against the random iteration statement logic that should maintain balance between the functions and external connections.

Core variable: [r] is the main variable that validates each function and every Iteration system.

mazeSize variable: [a] is the perimeter and propagated inner mazeSize of the perimeter, hence: (a^2)

Main Iteration variable: [b] is represented as main Wall 1 and main wall2 iterations: (b+b) of the mazeSize: (a^2) Sub Iteration variables of [b]: [Sw] is the random seeding iterations of main independent sub branch walls attached to the main walls. [Sw^n] is the random seeding iterations of independent sub branch walls of the main sub branch walls attached to the main sub branch walls.

Division by 2: [/2]: (Sw)+(Sw^n)+(((b+b)*(a^2))/2), validates the resulting global function variable: r of the two main wall system iterations when used across functions or externally.

Parameter checking with r: If [r] was connected to other function parameters of the Lead Edge Algorithm as a core accessor changing the value and state of r should be proportionally reflected in the Algorithm across all functions and external connections.

Lead Edge Algorithm Generation Parameter Logic Execution Number and Color Order:

Execution 1 Blue:

Define the Box Perimeter that consist of Two Perimeter Walls that leave an 1 entry on any side at random and 1 exit on any side at random but the the entry and exit must not come closer than one unit apart, as each wall will be 1 unit thick leaving the path 1 unit thick.

Math: D1 first b iteration [wall 1: (((b+b)(a^2))] D1 second iteration [wall 2: (((b+b)(a^2))]

Execution 2 Green:

Branches iterate off b for each wall with random lengths and turns but never touch one another or turn in on themselves. The perimeter branch corners and end corners must be no less than 1 unit apart and no further than 1 unit apart just with the rest of the wall geometry of the 2 perimeter walls and their branch geometry.

Math: D2 The Path: (Sw)+(Sw^n)+(((b+b)*(a^2))/2)=r Where divided by two is both D1 wall iterations and r is the proportional path.

D1 first b iteration [wall 1: (((b+b)(a^2))] D1 second iteration [wall 2: (((b+b)(a^2))] Then Branch Iterations: (Sw) and Sub Branch Iterations: (Sw^n)

Execution 3 Brown:

The two wall systems with the branch iterations extending off each of the 2 perimeter walls inwards with the perimeter never touch each other while they each are 1 unit thick leaving the path from entry to exit 1 unit thick. Each branch extending off each perimeter wall that does not directly contribute to the solvable path will eventually come to a dead end.

Offsetting the Algorithm and using the same Algorithm for each procedure: [(Sw)+(Sw^n)+(((b+b)*(a^2))/2)=r]:

The Lead Edge Algorithm achieves the same thing any other algorithm ever could due to the nature of a computer's binary logic of zero and one. This is possible because all it does is set up an even area to work within and then uses itself again as an offset of which it started with, a random activity, so it averages itself against itself with the previous thing achieved as an offset and therefore you have a finite factor to work with using the same algorithm. Lead Edge core Algebra at this point can become a placeholder variable for randomization then offset the next thing to do such as segmentation and then turns and so forth while maintaining the initial working canvas area achieved with algorithm and placing the additional maze generation assets in the initial canvas at random. So each asset to a maze’s generation is assembled separately based off the initial achievement of the canvas size and grid area at random then all is reassembled into that initial area at random while maintaining no less than two openings and no more than two openings and the openings cannot be directly in view of one another as well the first subpath off the solvable path must come before either of the openings are viewable, further the segments that make up each of the p aths and the perimeter can only be one unit in length and no more than one unit apart and no greater and no less than one year apart from one another at any given position while maintaining there are no islands of space segments and no island wall segments. So with that said the algorithm itself such as when divided by r should be equal to the overall generated maze and its foundation or equal to itself when used as itself to solve through the finished generated maze as Pathfinding.