Skip to content

isosurface.scad

Jump to bottom
Adrian Mariano edited this page Jun 3, 2025 · 1 revision

LibFile: isosurface.scad

Metaballs (also known as "blobby objects"), are bounded and closed organic surfaces that smoothly blend together. Metaballs are a specific kind of isosurface.

An isosurface, or implicit surface, is a three-dimensional surface representing all points of a constant value (e.g. pressure, temperature, electric potential, density) in a 3D volume. It's the 3D version of a 2D contour; in fact, any 2D cross-section of an isosurface is a 2D contour.

For computer-aided design, isosurfaces of abstract functions can generate complex curved surfaces and organic shapes. For example, spherical metaballs can be formulated using a set of point centers that define the metaball locations. For each metaball, a function is defined to compute the contribution of the metaball to any point in a 3D volume. The combined contributions from all the metaballs results in a function that varies in a complicated way throughout the volume. When two metaballs are far apart, they appear simply as spheres, but when they are close together they enlarge, reach toward each other, and meld together in a smooth fashion. The resulting metaball model appears as smoothly blended blobby shapes. The implementation below provides metaballs of a variety of types including spheres, cuboids, and cylinders (cones), with optional parameters to adjust the influence of one metaball on others, and the cutoff distance where the metaball's influence stops.

In general, an isosurface can be defined using any function of three variables $x, y, z$. The isosurface of a function $f(x,y,z)$ is the set of points where $f(x,y,z)=c$ for some constant value $c$. Such a function is also known as an "implicit surface" because the function implies a surface of constant value within a volume of space. The constant $c$ is referred to as the "isovalue". Changing the isovalue changes the position of the isosurface, depending on how the function is defined. Because metaballs are isosurfaces, they also have an isovalue. The isovalue is also known as the "threshold".

Some isosurface functions are unbounded, extending infinitely in all directions. A familiar example may be a gryoid, which is often used as a volume infill pattern in fused filament fabrication. The gyroid isosurface is unbounded and periodic in all three dimensions.

This file provides modules and functions to create a VNF using metaballs, or from general isosurfaces. This file also provides modules and functions to create 2d metaballs and contours, where the output is a list of paths, which can be open or closed paths.

For isosurfaces and 3D metaballs, the point list in the generated VNF structure contains many duplicated points. This is normally not a problem for rendering the shape, but machine roundoff differences may result in Manifold issuing warnings when doing the final render, causing rendering to abort if you have enabled the "stop on first warning" setting. You can prevent this by passing the VNF through vnf_quantize() using a quantization of 1e-7, or you can pass the VNF structure into vnf_merge_points(), which also removes the duplicates. Additionally, flat surfaces (often resulting from clipping by the bounding box) are triangulated at the voxel size resolution, and these can be unified into a single face by passing the vnf structure to vnf_unify_faces(). These steps can be computationally expensive and are not normally necessary.

To use, add the following lines to the beginning of your file:

include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>

File Contents

  1. Section: Metaballs

    • metaballs() – Creates a group of 3D metaballs (smoothly connected blobs). [Geom] [VNF]
    • metaballs2d() – Creates a group of 2D metaballs (smoothly connected blobs). [Geom] [Region]

  2. Section: Isosurfaces (3D) and contours (2D)

    • isosurface() – Creates a 3D isosurface (a 3D contour) from a function or array of values. [Geom] [VNF]
    • contour() – Creates a 2D contour from a function or array of values. [Geom] [Path] [Region]

Section: Metaballs

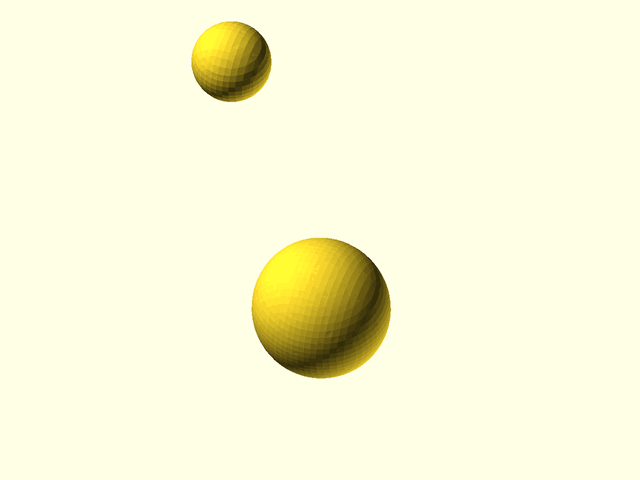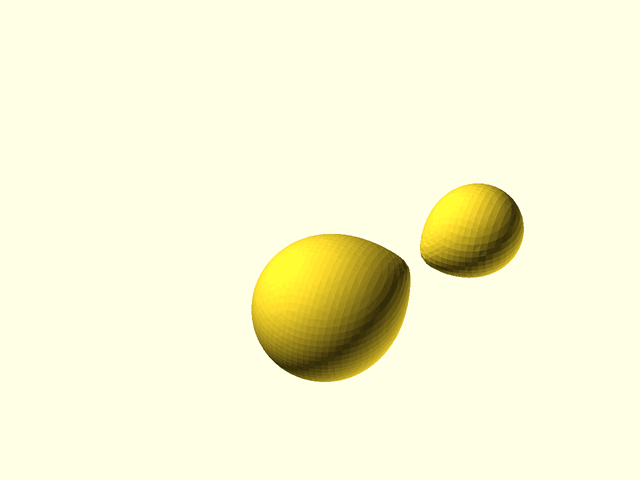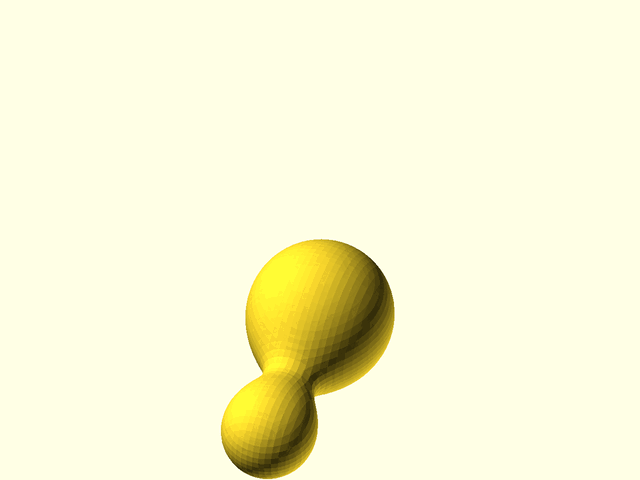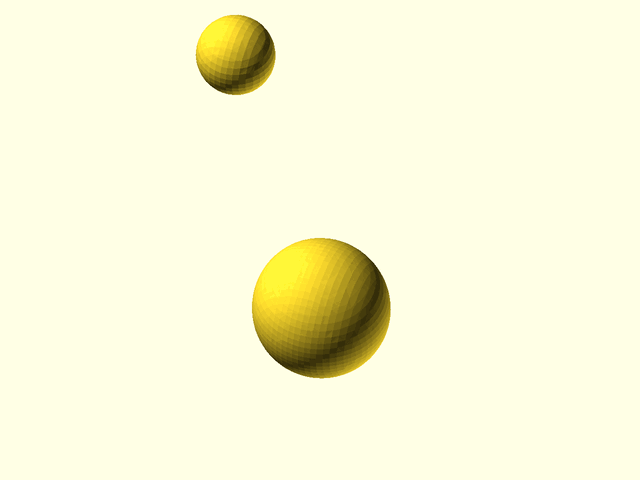
Metaball animation

Metaballs, also known as "blobby objects", can produce smoothly varying blobs and organic forms. You create metaballs by placing metaball objects at different locations. These objects have a basic size and shape when placed in isolation, but if another metaball object is nearby, the two objects interact, growing larger and melding together. The closer the objects are, the more they blend and meld.

The metaballs() module and function produce scenes of 3D metaballs. The metaballs2d() module and function produces scenes of 2D metaballs. The metaball specification method, tranformations, bounding box, and other parameters are used the say way in 3D and 2D, but in 2D, pixels replace voxels. This introductory section describes features common to both 3D and 2D cases.

Parameters common to 3D and 2D metaballs

Parameter spec: The simplest metaball specification is a 1D list of alternating transformation matrices and metaball functions: [trans0, func0, trans1, func1, ... ], passed as the spec parameter. Each transformation matrix you supply can be constructed using the usual transformation commands such as up(), right(), back(), move(), scale(), rot() and so on. You can multiply the transformations together, similar to how the transformations can be applied to regular objects in OpenSCAD. For example, to transform an object in regular OpenSCAD you might write up(5) zrot(45) scale(4). You would provide that transformation as the transformation matrix up(5) * zrot(45) * scale(4). You can use scaling to produce an ellipsoid from a sphere, and you can even use skew() if desired. When no transformation is needed, give IDENT as the transformation.

The spec parameter is flexible. It doesn't have to be just a list of alternating transformation matrices and metaball functions. It can also be a list of alternating transforms and other specs, as [trans0, spec0, trans1, spec1, ...], in which spec0, spec1, etc. can be one of:

  • A built-in metaball function name as described below, such as mb_sphere(r=10).
  • A function literal accepting a vector representing a point in space relative to the metaball's center.
  • An array containing a function literal and a debug VNF, as [custom_func, [sign, vnf]], where sign is the sign of the metaball and vnf is the VNF to show in the debug view when debug=true is set.
  • Another spec array, for nesting metaball specs together.

Nested metaball specs allow for complicated assemblies in which you can arrange components in a logical way, or repeat a structure with different transformation matrices. That is, instead of specifying a transform and function, you specify a transform and then another metaball specification. For example, you could set finger=[t0,f0,t1,f1,t2,f2] and then set hand=[u0,finger,u1,finger,...] and then invoke metaballs() with spec=[s0, hand]. In effect, any metaball specification array can be treated as a single metaball in another specification array. This is a powerful technique that lets you make groups of metaballs that you can use as individual metaballs in other groups, and can make your code compact and simpler to understand. Keep in mind that nested components aren't independent; they still interact with all other components. See Example 24.

Parameters bounding_box and grid units: The metaballs are evaluated over a bounding box. The bounding_box parameter can be specified by its minimum and maximum corners: [[xmin,ymin,zmin],[xmax,ymax,zmax]] in 3D, or [[xmin,ymin],[xmax,ymax]] in 2D. The bounding box can also be specified as a scalar size of a cube (in 3D) or square (in 2D) centered on the origin. The contributions from all metaballs, even those outside the box, are evaluated over the bounding box.

This bounding box is divided into grid units, specified as voxel_size in 3D or pixel_size in 2D, which can be a scalar or a vector size. Alternately, you can set the grid count (voxel_count or pixel_count) to fit approximately the specified number of grid units into the bounding box.

Objects in the scene having any dimension smaller than the grid spacing may not be displayed, so if objects seem to be missing, try making the grid units smaller or the grid count larger. By default, if the voxel size or pixel size doesn't exactly divide your specified bounding box, then the bounding box is enlarged to contain whole grid units, and centered on your requested box. Alternatively, you may set exact_bounds=true, which causes the grid units to adjust to fit instead, resulting in non-square grid units. Either way, if the bounding box clips a metaball and closed=true (the default), the object is closed at the intersection. Setting closed=false causes the object to end at the bounding box. In 3D, this results in a non-manifold shape with holes, exposing the inside of the object. In 2D, this results in an open-ended contour path with higher values on the right with respect to the path direction.

For metaballs with flat surfaces or sides, avoid letting any side of the bounding box coincide with one of these flat surfaces or sides, otherwise unpredictable triangulation around the edge may result.

Parameter isovalue: The isovalue parameter applies globally to all your metaballs and changes the appearance of your entire metaball object, possibly dramatically. It defaults to 1 and you don't usually need to change it. If you increase the isovalue, then all the objects in your model shrink, causing some melded objects to separate. If you decrease it, each metaball grows and melds more with others. As with isosurface(), a range may be specified for isovalue, which can result in hollow metaballs, although this isn't particularly useful except possibly in 2D.

Metaballs debug view

The module form of metaballs() and metaballs2d() can take a debug argument. When you set debug=true, the scene is rendered as a transparency (in 3D) or outline (in 2D) with the primitive metaball shapes shown inside, colored blue for positive, orange for negative, or gray for custom metaballs with no sign specified. These shapes are displayed at the sizes specified by the dimensional parameters in the corresponding metaball functions, regardless of isovalue. Setting hide_debug=true in individual metaball functions hides primitive shape from the debug view. Regardless the debug setting, child modules can access the metaball geometry via $metaball_vnf in 3D, or $metaball_pathlist in 2D.

User-defined metaball functions are displayed by default as gray tetrahedrons (3D) or triangles (2D) with a corner radius of 5, unless you also designate a shape for your custom function, as described below in the documentation for metaballs() and metaballs2d().

Metaballs run time

The size of the grid units (voxels or pixels) and size of the bounding box affects the run time, which can be long, especially in 3D. Smaller grid units produce a finer, smoother result at the expense of execution time. Larger grid units shorten execution time. The affect on run time is most evident for 3D metaballs, less so for 2D metaballs.

For example, in 3D, a voxel size of 1 with a bounding box volume of 200×200×200 may be slow because it requires the calculation and storage of eight million function values, and more processing and memory to generate the triangulated mesh. On the other hand, a voxel size of 5 over a 100×100×100 bounding box requires only 8,000 function values and a modest computation time. A good rule is to keep the number of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. If you don't specify voxel_size or voxel_count, then a default count of 10,000 voxels is used, which should be reasonable for initial preview.

In 2D, If you don't specify pixel_size or pixel_count, then a default count of 1024 pixels is used, which is reasonable for initial preview. You may find, however, that 2D metaballs are reasonably fast even at finer resolution.

Because a bounding box that is too large wastes time computing function values that are not needed, you can also set the parameter show_stats=true to get the actual bounds of the voxels intersected by the surface. With this information, you may be able to decrease run time, or keep the same run time but increase the resolution.

Metaball functions and user defined functions

You can construct complicated metaball models using only the built-in metaball functions described in the documentation below for metaballs() and metaballs2d(). However, you can create your own custom metaballs if desired.

When multiple metaballs are in a model, their functions are summed and compared to the isovalue to determine the final shape of the metaball object. Each metaball is defined as a function of a vector that gives the value of the metaball function for that point in space. As is common in metaball implementations, we define the built-in metaballs using an inverse relationship where the metaball functions fall off as $1/d$, where $d$ is distance measured from the center or core of the metaball. The 3D spherical metaball and 2D circular metaball therefore have a simple basic definition as $f(v) = 1/\text{norm}(v)$. If we choose an isovalue $c$, then the set of points $v$ such that $f(v) &gt;= c$ defines a bounded set; for example, a sphere with radius depending on the isovalue $c$. The default isovalue is $c=1$. Increasing the isovalue shrinks the object, and decreasing the isovalue grows the object.

To adjust interaction strength, the influence parameter applies an exponent, so if influence=a then the decay becomes $1/d^{1/a}$. This means, for example, that if you set influence to 0.5 you get a $1/d^2$ falloff. Changing this exponent changes how the balls interact.

You can pass a custom function as a function literal that takes a vector as its first argument and returns a single numerical value. Generally, the function should return a scalar value that drops below the isovalue somewhere within your bounding box. If you want your custom metaball function to behave similar to to the built-in functions, the return value should fall off with distance as $1/d$. See metaballs() Examples 20, 21, and 22 for demonstrations of creating custom metaball functions. Example 22 also shows how to make a complete custom metaball function that handles the influence and cutoff parameters.

By default, when debug=true, a custom 3D metaball function displays a gray tetrahedron with corner radius 5, and a custom 2D metaball function displays a gray triangle with corner radius 5. To specify a custom VNF for a custom function literal, enclose it in square brackets to make a list with the function literal as the first element, and another list as the second element, for example:

[ function (point) custom_func(point, arg1,...), [sign, vnf] ]

where sign is the sign of the metaball and vnf is the VNF to show in the debug view when debug=true. For 2D metaballs, you would specify a polygon path instead of a VNF. The sign determines the color of the debug object: 1 is blue, -1 is orange, and 0 is gray. See metaballs() Example 31 below for a demonstration of setting a VNF for a custom function.

Function/Module: metaballs()

Synopsis: Creates a group of 3D metaballs (smoothly connected blobs). [Geom] [VNF]

Topics: Metaballs, Isosurfaces, VNF Generators

See Also: isosurface()

Usage: As a module

  • metaballs(spec, bounding_box, voxel_size, [isovalue=], [closed=], [exact_bounds=], [convexity=], [show_stats=], [show_box=], [debug=] ...) [ATTACHMENTS];

Usage: As a function

  • vnf = metaballs(spec, bounding_box, voxel_size, [isovalue=], [closed=], [exact_bounds=], [convexity=], [show_stats=]);

Description:

Computes a VNF structure of a 3D metaball scene within a specified bounding box.

See metaball parameters for details on the primary parameters common to metaballs() and metaballs2d(). The spec parameter is described in more detail there. The spec parameter is a 1D list of alternating transforms and metaball functions; for example, the array spec= [ left(9), mb_sphere(5), right(9), mb_sphere(5) ] defines a scene with two spheres of radius 5 shifted 9 units to the left and right of the origin. The spec parameter completely defines the metaballs in your scene, including their position, orientation, and scaling, as well as different shapes.

You can create metaballs in a variety of standard shapes using the predefined functions listed below. If you wish, you can also create custom metaball shapes using your own functions (see Examples 20 and 21). For all of the built-in metaballs, three parameters are available to control the interaction of the metaballs with each other: cutoff, influence, and negative. These parameters apply to the individual metaball functions specified in your spec array; they are not parameters of metaballs().

The cutoff parameter specifies the distance beyond which the metaball has no interaction with other balls. When you apply cutoff, a smooth suppression factor begins decreasing the interaction strength at half the cutoff distance and reduces the interaction to zero at the cutoff. Note that the smooth decrease may cause the interaction to become negligible closer than the actual cutoff distance, depending on the voxel size and influence of the ball. Also, depending on the value of influence, a cutoff that ends in the middle of another ball can result in strange shapes, as shown in Example 17, with the metaball interacting on one side of the boundary and not interacting on the other side. If you scale a ball, the cutoff value is also scaled.

The influence parameter adjusts the strength of the interaction that metaball objects have with each other. If you increase influence of one metaball from its default of 1, then that metaball interacts with others at a longer range, and surrounding balls grow bigger. The metaball with larger influence can also grow bigger because it couples more strongly with other nearby balls, but it can also remain nearly unchanged while influencing others when isovalue is greater than 1. Decreasing influence has the reverse effect. Small changes in influence can have a large effect; for example, setting influence=2 dramatically increases the interactions at longer distances, and you may want to set the cutoff argument to limit the range influence. At the other exteme, small influence values can produce ridge-like artifacts or texture on the model. Example 14 demonstrates this effect. To avoid these artifacts, keep influence above about 0.5 and consider using cutoff instead of using small influence.

The negative parameter, if set to true, creates a negative metaball, which can result in hollows, dents, or reductions in size of other metaballs. Negative metaballs are never directly visible; only their effects are visible. The influence argument may also behave in ways you don't expect with a negative metaball. See Examples 16 and 17.

Built-in metaball functions

Several metaballs are defined for you to use in your models. All of the built-in metaballs take positional and named parameters that specify the size of the metaball (such as height or radius). The size arguments are the same as those for the regular objects of the same type (e.g. a sphere accepts both r for radius and the named parameter d= for diameter). The size parameters always specify the size of the metaball in isolation with isovalue=1. The metaballs can grow much bigger than their specified sizes when they interact with each other. Changing isovalue also changes the sizes of metaballs. They grow bigger than their specified sizes, even in isolation, if isovalue < 1 and smaller than their specified sizes if isovalue > 1.

The built-in metaball functions are listed below. As usual, arguments without a trailing = can be used positionally; arguments with a trailing = must be used as named arguments.

  • mb_sphere(r|d=) — spherical metaball, with radius r or diameter d. You can create an ellipsoid using scale() as the last transformation entry of the metaball spec array.
  • mb_cuboid(size, [squareness=]) — cuboid metaball with rounded edges and corners. The corner sharpness is controlled by the squareness parameter ranging from 0 (spherical) to 1 (cubical), and defaults to 0.5. The size parameter specifies the dimensions of the cuboid that circumscribes the rounded shape, which is tangent to the center of each cube face. The size parameter may be a scalar or a vector, as in cuboid(). Except when squareness=1, the faces are always a little bit curved.
  • mb_cyl(h|l|height|length, [r|d=], [r1=|d1=], [r2=|d2=], [rounding=]) — vertical cylinder or cone metaball with the same dimensional arguments as cyl(). At least one of the radius or diameter arguments is required. The rounding argument defaults to 0 (sharp edge) if not specified. Only one rounding value is allowed: the rounding is the same at both ends. For a fully rounded cylindrical shape, consider using mb_disk() or mb_capsule(), which are less flexible but have faster execution times.
  • mb_disk(h|l|height|length, r|d=) — flat disk with rounded edge, using the same dimensional arguments as cyl(). The diameter specifies the total diameter of the shape including the rounded sides, and must be greater than its height.
  • mb_capsule(h|l|height|length, [r|d=] — vertical cylinder with rounded caps, using the same dimensional arguments as cyl(). The object is a convex hull of two spheres. The height or length specifies the distance between the ends of the hemispherical caps.
  • mb_connector(p1, p2, [r|d=]) — a connecting rod of radius r or diameter d with hemispherical caps (like mb_capsule()), but specified to connect point p1 to point p2 (which must be different 3D coordinates). As with mb_capsule(), the object is a convex hull of two spheres. The points p1 and p2 are at the centers of the two round caps. The connectors themselves are still influenced by other metaballs, but it may be undesirable to have them influence others, or each other. If two connectors are connected, the joint may appear swollen unless influence or cutoff is reduced. Reducing cutoff is preferable if feasible, because reducing influence can produce interpolation artifacts.
  • mb_torus([r_maj|d_maj=], [r_min|d_min=], [or=|od=], [ir=|id=]) — torus metaball oriented perpendicular to the z axis. You can specify the torus dimensions using the same arguments as torus(); that is, major radius (or diameter) with r_maj or d_maj, and minor radius and diameter using r_min or d_min. Alternatively you can give the inner radius or diameter with ir or id and the outer radius or diameter with or or od. You must provide a combination of inputs that completely specifies the torus. If cutoff is applied, it is measured from the circle represented by r_min=0.
  • mb_octahedron(size, [squareness=]) — octahedron metaball with rounded edges and corners. The corner sharpness is controlled by the squareness parameter ranging from 0 (spherical) to 1 (sharp), and defaults to 0.5. The size parameter specifies the tip-to-tip distance of the octahedron that circumscribes the rounded shape, which is tangent to the center of each octahedron face. The size parameter may be a scalar or a vector, as in octahedron(). At squareness=0, the shape reduces to a sphere curcumscribed by the octahedron. Except when squareness=1, the faces are always curved.

In addition to the dimensional arguments described above, all of the built-in functions accept the following named arguments:

  • cutoff — positive value giving the distance beyond which the metaball does not interact with other balls. Cutoff is measured from the object's center. Default: INF
  • influence — a positive number specifying the strength of interaction this ball has with other balls. Default: 1
  • negative — when true, creates a negative metaball. Default: false
  • hide_debug — when true, suppresses the display of the underlying metaball shape when debug=true is set in the metaballs() module. This is useful to hide shapes that may be overlapping others in the debug view. Default: false

Duplicated vertices

The point list in the generated VNF structure contains many duplicated points. This is normally not a problem for rendering the shape, but machine roundoff differences may result in Manifold issuing warnings when doing the final render, causing rendering to abort if you have enabled the "stop on first warning" setting. You can prevent this by passing the VNF through vnf_quantize() using a quantization of 1e-7, or you can pass the VNF structure into vnf_merge_points(), which also removes the duplicates. Additionally, flat surfaces (often resulting from clipping by the bounding box) are triangulated at the voxel size resolution, and these can be unified into a single face by passing the vnf structure to vnf_unify_faces(). These steps can be computationally expensive and are not normally necessary.

Arguments:

By Position What it does
spec Metaball specification in the form [trans0, spec0, trans1, spec1, ...], with alternating transformation matrices and metaball specs, where spec0, spec1, etc. can be a metaball function or another metaball specification. See above for more details, and see Example 24 for a demonstration.
bounding_box The volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points [[xmin,ymin,zmin], [xmax,ymax,zmax]] specifying the minimum and maximum box corner coordinates. Unless you set exact_bounds=true, the bounding box size may be enlarged to fit whole voxels.
voxel_size Size of the voxels used to sample the bounding box volume, can be a scalar or 3-vector, or omitted if voxel_count is set. You may get a non-cubical voxels of a slightly different size than requested if exact_bounds=true.
By Name What it does
voxel_count Approximate number of voxels in the bounding box. If exact_bounds=true then the voxels may not be cubes. Use with show_stats=true to see the corresponding voxel size. Default: 10000 (if voxel_size not set)
isovalue A scalar value specifying the isosurface value (threshold value) of the metaballs. At the default value of 1.0, the internal metaball functions are designd so the size arguments correspond to the size parameter (such as radius) of the metaball, when rendered in isolation with no other metaballs. You can also specify an isovalue range such as [1,1.1], which creates hollow metaballs, where the hollow is evident when clipped by the bounding box. A scalar isovalue is equivalent to the range [isovalue,INF]. Default: 1.0
closed When true, close the surface if it intersects the bounding box by adding a closing face. When false, do not add a closing face, possibly producing non-manfold metaballs with holes where the bounding box intersects them. Default: true
exact_bounds When true, shrinks voxels as needed to fit whole voxels inside the requested bounding box. When false, enlarges bounding_box as needed to fit whole voxels of voxel_size, and centers the new bounding box over the requested box. Default: false
show_stats If true, display statistics about the metaball isosurface in the console window. Besides the number of voxels that the surface passes through, and the number of triangles making up the surface, this is useful for getting information about a possibly smaller bounding box to improve speed for subsequent renders. Enabling this parameter has a small speed penalty. Default: false
convexity (Module only) Maximum number of times a line could intersect a wall of the shape. Affects preview only. Default: 6
show_box (Module only) Display the requested bounding box as transparent. This box may appear slightly different than specified if the actual bounding box had to be expanded to accommodate whole voxels. Default: false
debug (Module only) Display the underlying primitive metaball shapes using your specified dimensional arguments, overlaid by the transparent metaball scene. Positive metaballs appear blue, negative appears orange, and any custom function with no debug VNF defined appears as a gray tetrahedron of corner radius 5.
cp (Module only) Center point for determining intersection anchors or centering the shape. Determines the base of the anchor vector. Can be "centroid", "mean", "box" or a 3D point. Default: "centroid"
anchor (Module only) Translate so anchor point is at origin (0,0,0). See anchor. Default: "origin"
spin (Module only) Rotate this many degrees around the Z axis after anchor. See spin. Default: 0
orient (Module only) Vector to rotate top toward, after spin. See orient. Default: UP
atype (Module only) Select "hull" or "intersect" anchor type. Default: "hull"

Anchor Types:

Anchor Type What it is
"hull" Anchors to the virtual convex hull of the shape.
"intersect" Anchors to the surface of the shape.

Named Anchors:

Anchor Name Position
"origin" Anchor at the origin, oriented UP.

Side Effects:

  • $metaball_vnf is set to the VNF of the metaball scene.

Example 1: Two spheres interacting.

metaballs() Example 1 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(9), mb_sphere(5),
    right(9), mb_sphere(5)
];
metaballs(spec, voxel_size=0.5,
    bounding_box=[[-16,-7,-7], [16,7,7]]);



Example 2: Two rounded cuboids interacting.

metaballs() Example 2 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    move([-8,-5,-5]), mb_cuboid(10),
    move([8,5,5]), mb_cuboid(10)
];
metaballs(spec, voxel_size=0.5,
    bounding_box=[[-15,-12,-12], [15,12,12]]);



Example 3: Two rounded mb_cyl() cones interacting.

metaballs() Example 3 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(10), mb_cyl(15, r1=6, r2=4, rounding=2),
    right(10), mb_cyl(15, r1=6, r2=4, rounding=2)
];
metaballs(spec, voxel_size=0.5,
    bounding_box=[[-17,-8,-10], [17,8,10]]);



Example 4: Two disks interacting. Here the arguments are in order and not named.

metaballs() Example 4 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
metaballs([
    move([-10,0,2]), mb_disk(5,9),
    move([10,0,-2]), mb_disk(5,9)
    ], [[-20,-10,-6], [20,10,6]], 0.5);



Example 5: Two capsules interacting.

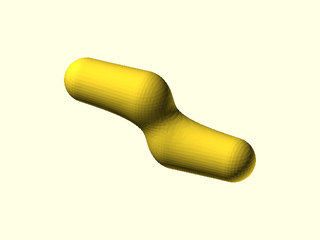
metaballs() Example 5 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
metaballs([
    move([-8,0,4])*yrot(90), mb_capsule(16,3),
    move([8,0,-4])*yrot(90), mb_capsule(16,3)
    ], [[-17,-5,-8], [17,5,8]],  0.5);



Example 6: A sphere with two connectors.

metaballs() Example 6 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
path = [[-20,0,0], [0,0,1], [0,-10,0]];
spec = [
    move(path[0]), mb_sphere(6),
    for(seg=pair(path)) each
       [IDENT, mb_connector(seg[0],seg[1],
        2, influence=0.5)]
];
metaballs(spec, voxel_size=0.5,
    bounding_box=[[-27,-13,-7], [4,7,14]]);



Example 7: Interaction between two tori in different orientations.

metaballs() Example 7 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    move([-10,0,17]),        mb_torus(r_maj=6, r_min=2),
    move([7,6,21])*xrot(90), mb_torus(r_maj=7, r_min=3)
];
voxel_size = 0.5;
boundingbox = [[-19,-9,9], [18,10,32]];
metaballs(spec, boundingbox, voxel_size);



Example 8: Two octahedrons interacting. Here voxel_size is not given, so it defaults to a value that results in approximately 10,000 voxels in the bounding box. Adding the parameter show_stats=true displays the voxel size used, along with other information.

metaballs() Example 8 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
metaballs([
    move([-11,0,4]), mb_octahedron(20),
    move([11,0,-4]), mb_octahedron(20)
    ], [[-21,-11,-14], [21,11,14]]);



Example 9: These next five examples demonstrate the different types of metaball interactions. We start with two spheres 30 units apart. Each would have a radius of 10 in isolation, but because they are influencing their surroundings, each sphere mutually contributes to the size of the other. The sum of contributions between the spheres add up so that a surface plotted around the region exceeding the threshold defined by isovalue=1 looks like a peanut shape surrounding the two spheres.

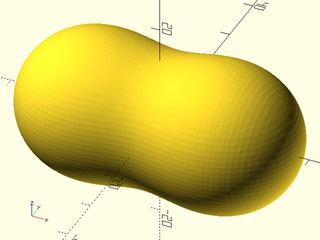
metaballs() Example 9 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(15),  mb_sphere(10),
    right(15), mb_sphere(10)
];
voxel_size = 1;
boundingbox = [[-30,-19,-19], [30,19,19]];
metaballs(spec, boundingbox, voxel_size);



Example 10: Adding a cutoff of 25 to the left sphere causes its influence to disappear completely 25 units away (5 units from the center of the right sphere). The left sphere is bigger because it still receives the full influence of the right sphere, but the right sphere is smaller because the left sphere has no contribution past 25 units. The right sphere is not abruptly cut off because the cutoff function is smooth and influence is normal. Setting cutoff too small can remove the interactions of one metaball from all other metaballs, leaving that metaball alone by itself.

metaballs() Example 10 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(15),  mb_sphere(10, cutoff=25),
    right(15), mb_sphere(10)
];
voxel_size = 1;
boundingbox = [[-30,-19,-19], [30,19,19]];
metaballs(spec, boundingbox, voxel_size);



Example 11: Here, the left sphere has less influence in addition to a cutoff. Setting influence=0.5 results in a steeper falloff of contribution from the left sphere. Each sphere has a different size and shape due to unequal contributions based on distance.

metaballs() Example 11 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(15),  mb_sphere(10, influence=0.5, cutoff=25),
    right(15), mb_sphere(10)
];
voxel_size = 1;
boundingbox = [[-30,-19,-19], [30,19,19]];
metaballs(spec, boundingbox, voxel_size);



Example 12: In this example, we have two size-10 spheres as before and one tiny sphere of 1.5 units radius offset a bit on the y axis. With an isovalue of 1, this figure would appear similar to Example 9 above, but here the isovalue has been set to 2, causing the surface to shrink around a smaller volume values greater than 2. Remember, higher isovalue thresholds cause metaballs to shrink.

metaballs() Example 12 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
   left(15),  mb_sphere(10),
   right(15), mb_sphere(10),
   fwd(15),   mb_sphere(1.5)
];
voxel_size = 1;
boundingbox = [[-30,-19,-19], [30,19,19]];
metaballs(spec, boundingbox, voxel_size,
    isovalue=2);



Example 13: Keeping isovalue=2, the influence of the tiny sphere has been set quite high, to 10. Notice that the tiny sphere shrinks a bit, but it has dramatically increased its contribution to its surroundings, causing the two other spheres to grow and meld into each other. The influence argument on a small metaball affects its surroundings more than itself.

metaballs() Example 13 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
   move([-15,0,0]), mb_sphere(10),
   move([15,0,0]),  mb_sphere(10),
   move([0,-15,0]), mb_sphere(1.5, influence=10)
];
voxel_size = 1;
boundingbox = [[-30,-19,-19], [30,19,19]];
metaballs(spec, boundingbox, voxel_size,
    isovalue=2);



Example 14: Setting influence to less than 0.5 can cause interpolation artifacts in the surface. The only difference between these two spheres is influence. Both have cutoff set to prevent them from affecting each other. The sphere on the right has a low influence of 0.02, which translates to a falloff with distance $d$ proportional to $1/d^{50}$. That high exponent increases the non-linear nature of the function gradient at the isosurface, reducing the accuracy of the linear interpolation of where the the surface intersects each voxel, causing ridges to appear. You could use this to create a texture deliberately, but it is usually better to use cutoff to limit the range of influence rather than reducing influence significantly below 1.

metaballs() Example 14 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(10), mb_sphere(8, cutoff=10, influence=1),
    right(10), mb_sphere(8, cutoff=10, influence=0.02)
];
bbox = [[-18,-8,-8], [18,8,8]];
metaballs(spec, bounding_box=bbox, voxel_size=0.4);

Example 15: A group of five spherical metaballs with different sizes. The parameter show_stats=true (not shown here) was used to find a compact bounding box for this figure. Here instead of setting voxel_size, we set voxel_count for approximate number of voxels in the bounding box, and the voxel size is adjusted to fit. Setting exact_bounds=true forces the bounding box to be fixed, and a non-cubic voxel is then used to fit within that box.

metaballs() Example 15 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [ // spheres of different sizes
    move([-20,-20,-20]), mb_sphere(5),
    move([0,-20,-20]),   mb_sphere(4),
    IDENT,               mb_sphere(3),
    move([0,0,20]),      mb_sphere(5),
    move([20,20,10]),    mb_sphere(7)
];
voxel_size = 1.5;
boundingbox = [[-30,-31,-31], [32,31,30]];
metaballs(spec, boundingbox,
    exact_bounds=true, voxel_count=40000);



Example 16: A metaball can be negative. In this case we have two metaballs in close proximity, with the small negative metaball creating a dent in the large positive one. The positive metaball is shown transparent, and small spheres show the center of each metaball. The negative metaball isn't visible because its field is negative; the isosurface encloses only field values greater than the isovalue of 1.

metaballs() Example 16 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
centers = [[-1,0,0], [1.25,0,0]];
spec = [
    move(centers[0]), mb_sphere(8),
    move(centers[1]), mb_sphere(3, negative=true)
];
voxel_size = 0.25;
boundingbox = [[-7,-6,-6], [3,6,6]];
%metaballs(spec, boundingbox, voxel_size);
color("green") move_copies(centers) sphere(d=1, $fn=16);



Example 17: When a positive and negative metaball interact, the negative metaball reduces the influence of the positive one, causing it to shrink, but not disappear because its contribution approaches infinity at its center. In this example we have a large positive metaball near a small negative metaball at the origin. The negative ball has high influence, and a cutoff limiting its influence to 20 units. The negative metaball influences the positive one up to the cutoff, causing the positive metaball to appear smaller inside the cutoff range, and appear its normal size outside the cutoff range. The positive metaball has a small dimple at the origin (the center of the negative metaball) because it cannot overcome the infinite negative contribution of the negative metaball at the origin.

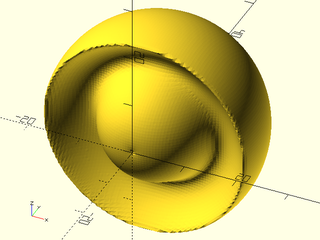
metaballs() Example 17 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    back(10), mb_sphere(20),
    IDENT, mb_sphere(2, influence=30,
        cutoff=20, negative=true),
];
voxel_size = 0.5;
boundingbox = [[-20,-4,-20], [20,30,20]];
metaballs(spec, boundingbox, voxel_size);



Example 18: A sharp cube, a rounded cube, and a sharp octahedron interacting. Because the surface is generated through cubical voxels, voxel corners are always cut off, resulting in difficulty resolving some sharp edges.

metaballs() Example 18 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    move([-7,-3,27])*zrot(55), mb_cuboid(6, squareness=1),
    move([5,5,21]),   mb_cuboid(5),
    move([10,0,10]),  mb_octahedron(10, squareness=1)
];
voxel_size = 0.5; // a bit slow at this resolution
boundingbox = [[-12,-9,3], [18,10,32]];
metaballs(spec, boundingbox, voxel_size);



Example 19: A toy airplane, constructed only from metaball spheres with scaling. The bounding box is used to clip the wingtips, tail, and belly of the fuselage.

metaballs() Example 19 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
bounding_box = [[-55,-50,-5],[35,50,17]];
spec = [
    move([-20,0,0])*scale([25,4,4]),   mb_sphere(1), // fuselage
    move([30,0,5])*scale([4,0.5,8]),   mb_sphere(1), // vertical stabilizer
    move([30,0,0])*scale([4,15,0.5]),  mb_sphere(1), // horizontal stabilizer
    move([-15,0,0])*scale([6,45,0.5]), mb_sphere(1)  // wing
];
voxel_size = 1;
color("lightblue") metaballs(spec, bounding_box, voxel_size);

Example 20: Custom metaballs are an advanced technique in which you define your own metaball shape by passing a function literal that takes a single argument: a coordinate in space relative to the metaball center called point here, but can be given any name. This distance vector from the origin is calculated internally and always passed to the function. Inside the function, it is converted to a scalar distance dist. The function literal expression sets all of your parameters. Only point is not set, and it becomes the single parameter to the function literal. The spec argument invokes your custom function as a function literal that passes point into it.

metaballs() Example 20 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function threelobe(point) =
   let(
        ang=atan2(point.y, point.x),
        r=norm([point.x,point.y])*(1.3+cos(3*ang)),
        dist=norm([point.z, r])
   ) 3/dist;
metaballs(
    spec = [
        IDENT, function (point) threelobe(point),
        up(7), mb_sphere(r=4)
    ],
    bounding_box = [[-14,-12,-5],[8,12,13]],
    voxel_size=0.5);



Example 21: Here is a function nearly identical to the previous example, introducing additional dimensional parameters into the function to control its size and number of lobes. The bounding box size here is as small as possible for calculation efficiency, but if you expiriment with this using different argument values, you should increase the bounding box along with voxel size.

metaballs() Example 21 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function multilobe(point, size, lobes) =
   let(
        ang=atan2(point.y, point.x),
        r=norm([point.x,point.y])*(1.3+cos(lobes*ang)),
        dist=norm([point.z, r])
   ) size/dist;
metaballs(
    spec = [
        left(7),
           function (point) multilobe(point, 3, 4),
        right(7)*zrot(60),
           function (point) multilobe(point, 3, 3)
    ],
    bounding_box = [[-16,-13,-5],[18,13,6]],
    voxel_size=0.4);



Example 22: Next we show how to create a function that works like the built-ins. This is a full implementation that allows you to specify the function directly by name in the spec argument without needing the function literal syntax, and without needing the point argument in spec, as in the prior examples. Here, noisy_sphere_calcs() is the calculation function that accepts the pointposition argument and any other parameters needed (hererandnoise_level), and returns a single value. Then there is a "master" function noisy_sphere() that does some error checking and returns an array consisting of (a) a function literal expression that sets all of your parameters, and (b) another array containing the metaball sign and a simple "debug" VNF representation of the metaball for viewing when debug=true is passed to metaballs(). The call to mb_cutoff() at the end handles the cutoff function for the noisy ball consistent with the other internal metaball functions; it requires dist and cutoff as arguments. You are not required to use this implementation in your own custom functions; in fact it's easier simply to declare the function literal in your spec argument, but this example shows how to do it all.

metaballs() Example 22 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
//
// noisy sphere internal calculation function

function noisy_sphere_calcs(point, r, noise_level, cutoff, exponent, neg) =
    let(
        noise = rands(0, noise_level, 1)[0],
        dist = norm(point) + noise // distance to point from metaball center
    ) neg * mb_cutoff(dist,cutoff) * (r/dist)^exponent;

// noisy sphere "master" entry function to use in spec argument

function noisy_sphere(r, noise_level, cutoff=INF, influence=1, negative=false, hide_debug=false, d) =
   assert(is_num(cutoff) && cutoff>0, "\ncutoff must be a positive number.")
   assert(is_finite(influence) && influence>0, "\ninfluence must be a positive number.")
   let(
       r = get_radius(r=r,d=d),
       dummy=assert(is_finite(r) && r>0, "\ninvalid radius or diameter."),
       neg = negative ? -1 : 1,
       // create [sign, vnf] for debug view; show tiny shape if hide_debug=true
       debug_vnf = [neg, hide_debug ? debug_tetra(0.02) : sphere(r, $fn=16)]
   ) [
       // pass control as a function literal to the calc function
       function (point) noisy_sphere_calcs(point, r, noise_level, cutoff, 1/influence, neg),
       debug_vnf
   ];

// define the scene and render it

spec = [
    left(9),  mb_sphere(5),
    right(9), noisy_sphere(r=5, noise_level=0.2)
];
voxel_size = 0.5;
boundingbox = [[-16,-8,-8], [16,8,8]];
metaballs(spec, boundingbox, voxel_size);

Example 23: Demonstration of debug=true with a more complex example using ellipsoids, a capsule, spheres, and a torus to make a tetrahedral object with rounded feet and a ring on top. The bottoms of the feet are flattened by clipping with the bottom of the bounding box. The center of the object is thick due to the contributions of three ellipsoids and a capsule converging. Designing an object like this using metaballs requires trial and error with low-resolution renders.

metaballs() Example 23 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
include <BOSL2/polyhedra.scad>
tetpts = zrot(15, p = 22 * regular_polyhedron_info("vertices", "tetrahedron"));
tettransform = [ for(pt = tetpts) move(pt)*rot(from=RIGHT, to=pt)*scale([7,1.5,1.5]) ];

spec = [
    // vertical cylinder arm
    up(15), mb_capsule(17, 2, influence=0.8),
    // ellipsoid arms
    for(i=[0:2]) each [tettransform[i], mb_sphere(1, cutoff=30)],
    // ring on top
    up(35)*xrot(90), mb_torus(r_maj=8, r_min=2.5, cutoff=35),
    // feet
    for(i=[0:2]) each [move(2.2*tetpts[i]), mb_sphere(5, cutoff=30)],
];
voxel_size = 1;
boundingbox = [[-22,-32,-13], [36,32,46]];
metaballs(spec, boundingbox, voxel_size, isovalue=1, debug=true);

Example 24: This example demonstrates grouping metaballs together and nesting them in lists of other metaballs, to make a crude model of a hand. Here, just one finger is defined, and a thumb is defined from one less joint in the finger. Individual fingers are grouped together with different positions and scaling, along with the thumb. Finally, this group of all fingers is used to combine with a rounded cuboid, with a slight ellipsoid dent subtracted to hollow out the palm, to make the hand.

metaballs() Example 24 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
joints = [[0,0,1], [0,0,85], [0,-5,125], [0,-16,157], [0,-30,178]];
finger = [
    for(i=[0:3]) each
        [IDENT, mb_connector(joints[i], joints[i+1], 9+i/5, influence=0.22)]
];
thumb = [
    for(i=[0:2]) each [
        scale([1,1,1.2]),
        mb_connector(joints[i], joints[i+1], 9+i/2, influence=0.28)
    ]
];
allfingers = [
    left(15)*zrot(5)*yrot(-50)*scale([1,1,0.6])*zrot(30), thumb,
    left(15)*yrot(-9)*scale([1,1,0.9]), finger,
    IDENT, finger,
    right(15)*yrot(8)*scale([1,1,0.92]), finger,
    right(30)*yrot(17)*scale([0.9,0.9,0.75]), finger
];
hand = [
    IDENT, allfingers,
    move([-5,0,5])*scale([1,0.36,1.55]), mb_cuboid(90, squareness=0.3, cutoff=80),
    move([-10,-95,50])*yrot(10)*scale([2,2,0.95]),
        mb_sphere(r=15, cutoff=50, influence=1.5, negative=true)
];
voxel_size=2.5;
bbox = [[-104,-40,-10], [79,18,188]];
metaballs(hand, bbox, voxel_size, isovalue=1);

Example 25: A model of an elephant using cylinders, capsules, and disks.

metaballs() Example 25 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
legD1 = 4.6;
legD2 = 1;
spec = [
    // legs
    up(1)*fwd(8)*left(13), mb_cyl(d1=legD1, d2=legD2, h=20),
    up(1)*fwd(8)*right(10), mb_cyl(d1=legD1, d2=legD2, h=20),
    up(1)*back(8)*left(13), mb_cyl(d1=legD1, d2=legD2, h=20),
    up(1)*back(8)*right(10), mb_cyl(d1=legD1, d2=legD2, h=20),
    up(20)*yrot(90), mb_capsule(d=21, h=36, influence=0.5), // body
    right(21)*up(25)*yrot(-20), mb_capsule(r=7, h=25, influence=0.5, cutoff=9), // head
    right(24)*up(10)*yrot(15), mb_cyl(d1=3, d2=6, h=15, cutoff=3), // trunk
    // ears
    right(18)*up(29)*fwd(11)*zrot(-20)*yrot(80)*scale([1.4,1,1]), mb_disk(r=5,h=2, cutoff=3),
    right(18)*up(29)*back(11)*zrot(20)*yrot(80)*scale([1.4,1,1]), mb_disk(r=5,h=2, cutoff=3),
    // tusks
    right(26)*up(13)*fwd(5)*yrot(135), mb_capsule(r=1, h=10, cutoff=1),
    right(26)*up(13)*back(5)*yrot(135), mb_capsule(r=1, h=10, cutoff=1)
];
bbox = [[-21,-17,-9], [31,17,38]];
metaballs(spec, bounding_box=bbox, voxel_size=1, isovalue=1);

Example 26: A model of a giraffe using a variety of different metaball shapes. Features such as the tail and lower legs are thin, so a small voxel size is required to render them.

metaballs() Example 26 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
legD = 1;
tibia = 14;
femur = 12;
head = [-35,0,78];  // head position
stance = [12,6];    // leg position offsets

spec = [
    // Lower legs
    move([-stance.x,-stance.y]), mb_connector([-4,0,0.25],[-6,0,tibia],legD, influence = 0.2),
    move([-stance.x,stance.y]),  mb_connector([0,0,0],[0,0,tibia],legD, influence = 0.2),
    move([stance.x,-stance.y]),  mb_connector([-2,0,0],[-3,0,tibia],legD, influence = 0.2),
    move([stance.x,stance.y]),   mb_connector([0,0,0],[0,0,tibia],legD, influence = 0.2),
    // Upper legs
    move([-stance.x,-stance.y,tibia]), mb_connector([-6,0,0],[-2,0,femur],legD),
    move([-stance.x,stance.y,tibia]),  mb_connector([0,0,0],[0,0,femur],legD),
    move([stance.x,-stance.y,tibia]),  mb_connector([-3,0,0],[-1,0,femur],legD),
    move([stance.x,stance.y,tibia]),   mb_connector([0,0,0],[0,0,femur],legD),

    // Hooves
    move([-stance.x-5.5,-stance.y,1.25])*yrot(-5), mb_capsule(d=2, h=3, cutoff=2),
    move([-stance.x-4.5,-stance.y,-1.4])*yrot(-5), mb_cuboid(size=4, squareness=1, cutoff=1, influence=20, negative=true), // truncate bottom of raised hoof
    move([-stance.x-1,stance.y,1]),     mb_capsule(d=2, h=3, cutoff=2),
    move([stance.x-3.5,-stance.y,1]),   mb_capsule(d=2, h=3, cutoff=2),
    move([stance.x-1,stance.y,1]),      mb_capsule(d=2, h=3, cutoff=2),

    // Body
    up(tibia+femur+10) * yrot(10),        mb_cuboid([16,7,7]),
    up(tibia+femur+15)*left(10),          mb_sphere(2),
    up(tibia+femur+8)*right(13)*xrot(90), mb_disk(1,4),

    // Tail
    up(tibia+femur+8), mb_connector([18,0,0],[22,0,-16], 0.4, cutoff = 1),

    // Neck
    up(tibia+femur+35)*left(22)*yrot(-30)* yscale(0.75), mb_cyl(d1 = 5, d2 = 3, l = 38),

    // Head
    move(head + [-4,0,-3])*yrot(45)*xscale(0.75), mb_cyl(d1 = 1.5, d2 = 4, l = 12, rounding=0),
    move(head), mb_cuboid(2),

    // Horns
    move(head), mb_connector([0,-2,5],[0,-2.5,8],0.3, cutoff = 1),
    move(head + [0,-2.5,8]), mb_sphere(0.5, cutoff = 1),
    move(head), mb_connector([0,2,5],[0,2.5,8],0.3, cutoff = 1),
    move(head + [0,2.5,8]), mb_sphere(0.5, cutoff = 1),

    // Ears
    move(head + [2,-8,4])* xrot(60) * scale([0.5,1,3]) , mb_sphere(d = 2, cutoff = 2),
    move(head + [2,8,4])* xrot(-60) * scale([0.5,1,3]) , mb_sphere(d = 2, cutoff = 2),
];
vsize = 0.85;
bbox =  [[-45.5, -11.5, 0], [23, 11.5, 87.55]];
metaballs(spec, bbox, voxel_size=vsize);

Example 27: A model of a bunny, assembled from separate body components made with metaballs, with each component rendered at a different voxel size, and then combined together along with eyes and teeth. In this way, smaller bounding boxes can be defined for each component, which speeds up rendering. A bit more time is saved by saving the repeated components (ear, front leg, hind leg) in VNF structures, to render copies with vnf_polyhedron().

metaballs() Example 27 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
torso = [
    up(20) * scale([1,1.2,2]), mb_sphere(10),
    up(10), mb_sphere(5) // fatten lower torso
];
head = [
    up(50) * scale([1.2,0.8,1]), mb_sphere(10, cutoff = 15),
    // nose
    move([0,-11,50]), mb_cuboid(2),
    // eye sockets
    move([5,-10,54]), mb_sphere(0.5, negative = true),
    move([-5,-10,54]), mb_sphere(0.5, negative = true),
    // tail
    move([0,15,6]), mb_sphere(2, cutoff = 5)
];
hind_leg = [
    move([-15,-5,3]) * scale([1.5,4,1.75]), mb_sphere(5),
    move([-15,10,3]), mb_sphere(3, negative = true)
];
front_leg = [
    move([-9,-4,30]) * zrot(30) * scale([1.5,5,1.75]), mb_sphere(3),
    move([-9,10,30]), mb_sphere(2, negative = true)
];
ear = [
    yrot(10) * move([0,0,65]) * scale([4,1,7]), mb_sphere(2),
    yrot(10)*move([0,-3,65])*scale([3,2,6]), mb_sphere(2, cutoff = 2, influence =2, negative = true)
];
vnf_hindleg = metaballs(hind_leg, [[-22,-24,0],[-8,7,11]], voxel_size=0.8);
vnf_frontleg = metaballs(front_leg, [[-16,-17,25], [-1,7,35]], voxel_size=0.6);
vnf_ear = metaballs(ear, [[3,-2,50],[20,2,78]], voxel_size=0.6);
color("BurlyWood") {
    metaballs([IDENT, torso, IDENT, head],
        [[-16,-17,0],[16,20,63]], voxel_size=0.7);
    xflip_copy() {
        vnf_polyhedron(vnf_hindleg);
        vnf_polyhedron(vnf_frontleg);
        vnf_polyhedron(vnf_ear);;
    }
}
// add eyes
xflip_copy() move([5,-8,54]) color("skyblue") sphere(2, $fn = 32);
// add teeth
xflip_copy() move([1.1,-10,44]) color("white") cuboid([2,0.5,4], rounding = 0.15);

Example 28: A model of a duck made from spheres, disks, a capsule, and a cone for the tail.

metaballs() Example 28 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
b_box = [[-31,-18,-10], [29,18,31]];
headZ = 21;
headX = 11;
spec = [
    // head
    left(headX)*up(headZ)*scale([1,0.9,1]), mb_sphere(10,cutoff=11), //skull
    left(headX)*up(14), mb_disk(3,5, influence=0.5), //neck shim
    left(headX+5)*up(headZ-1)*fwd(5),  mb_disk(1,2, cutoff=4), //cheek bulge
    left(headX+5)*up(headZ-1)*back(5), mb_disk(1,2, cutoff=4), //cheek bulge
    // eye indentations
    move([-headX,0,headZ+3])*zrot(70)*left(9)*yrot(25)*scale([1,3,1.3]), mb_sphere(1, negative=true, influence=1, cutoff=10),
    move([-headX,0,headZ+3])*zrot(-70)*left(9)*yrot(25)*scale([1,3,1.3]), mb_sphere(1, negative=true, influence=1, cutoff=10),
    // beak
    left(headX+13)*up(headZ)*zscale(0.4)*yrot(90), mb_capsule(12,3, cutoff=5),
    left(headX+8)*up(headZ), mb_disk(2,4),
    left(headX+16)*up(30), mb_sphere(5, negative=true, cutoff=8),
    left(headX+12)*up(headZ+1)*scale([1.2,1,0.75]), mb_sphere(2, cutoff = 3),
    // body
    scale([1.5,1,1]), mb_disk(17,15), //body
    // tail
    right(20)*up(8)*yscale(1.7)*yrot(35), mb_cyl(h=15, r1=4, r2=0.5)
];
metaballs(spec, b_box, voxel_size=0.75);
// add eyeballs
yflip_copy()
    move([-headX,0,headZ+2.5])zrot(53)left(4.9) color("#223300") sphere(3,$fn=64);

Example 29: Specifying debug=true, we can see the elements used to construct the duck. Positive metaballs are blue and negative metaballs are orange. Unfortunately, although the head is a rather complex structure, the big blue skull element covers up other details. Note also that removing the voxel_size parameter from metaballs() speeds up the preview.

metaballs() Example 29 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
b_box = [[-31,-18,-10], [29,18,31]];
headZ = 21;
headX = 11;
spec = [
    // head
    left(headX)*up(headZ)*scale([1,0.9,1]), mb_sphere(10,cutoff=11), //skull
    left(headX)*up(14), mb_disk(3,5, influence=0.5), //neck shim
    left(headX+5)*up(headZ-1)*fwd(5),  mb_disk(1,2, cutoff=4), //cheek bulge
    left(headX+5)*up(headZ-1)*back(5), mb_disk(1,2, cutoff=4), //cheek bulge
    // eye indentations
    move([-headX,0,headZ+3])*zrot(70)*left(9)*yrot(25)*scale([1,3,1.3]), mb_sphere(1, negative=true, influence=1, cutoff=10),
    move([-headX,0,headZ+3])*zrot(-70)*left(9)*yrot(25)*scale([1,3,1.3]), mb_sphere(1, negative=true, influence=1, cutoff=10),
    // beak
    left(headX+13)*up(headZ)*zscale(0.4)*yrot(90), mb_capsule(12,3, cutoff=5),
    left(headX+8)*up(headZ), mb_disk(2,4),
    left(headX+16)*up(30), mb_sphere(5, negative=true, cutoff=8),
    left(headX+12)*up(headZ+1)*scale([1.2,1,0.75]), mb_sphere(2, cutoff = 3),
    // body
    scale([1.5,1,1]), mb_disk(17,15), //body
    // tail
    right(20)*up(8)*yscale(1.7)*yrot(35), mb_cyl(h=15, r1=4, r2=0.5)
];
metaballs(spec, b_box, debug=true); // removed voxel_size, set debug=true
// add eyeballs
yflip_copy()
    move([-headX,0,headZ+2.5])zrot(53)left(4.9) color("#223300") sphere(3,$fn=64);

Example 30: Adding hide_debug=true to the skull metaball function suppresses its display and reveals the neck and cheek components formerly covered by the skull metaball. Here we also disabled the addition of eyeballs, and reduced the size of the bounding box to enclose only the head. The bounding box is for computing the metaball surface; the debug components still display outside these bounds.

metaballs() Example 30 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
b_box = [[-31,-18,11], [0,18,31]];
headZ = 21;
headX = 11;
spec = [
    // head
    left(headX)*up(headZ)*scale([1,0.9,1]), mb_sphere(10,cutoff=11,hide_debug=true), //skull
    left(headX)*up(14), mb_disk(3,5, influence=0.5), //neck shim
    left(headX+5)*up(headZ-1)*fwd(5),  mb_disk(1,2, cutoff=4), //cheek bulge
    left(headX+5)*up(headZ-1)*back(5), mb_disk(1,2, cutoff=4), //cheek bulge
    // eye indentations
    move([-headX,0,headZ+3])*zrot(70)*left(9)*yrot(25)*scale([1,3,1.3]), mb_sphere(1, negative=true, influence=1, cutoff=10),
    move([-headX,0,headZ+3])*zrot(-70)*left(9)*yrot(25)*scale([1,3,1.3]), mb_sphere(1, negative=true, influence=1, cutoff=10),
    // beak
    left(headX+13)*up(headZ)*zscale(0.4)*yrot(90), mb_capsule(12,3, cutoff=5),
    left(headX+8)*up(headZ), mb_disk(2,4),
    left(headX+16)*up(30), mb_sphere(5, negative=true, cutoff=8),
    left(headX+12)*up(headZ+1)*scale([1.2,1,0.75]), mb_sphere(2, cutoff = 3),
    // body
    scale([1.5,1,1]), mb_disk(17,15), //body
    // tail
    right(20)*up(8)*yscale(1.7)*yrot(35), mb_cyl(h=15, r1=4, r2=0.5)
];
metaballs(spec, b_box, debug=true); // removed voxel_size, set debug=true
// add eyeballs
* yflip_copy()
    move([-headX,0,headZ+2.5])zrot(53)left(4.9) color("#223300") sphere(3,$fn=64);

Example 31: Adapting the multi-lobe function from Example 21 above, here we show how to display a debug-view VNF approximating the shape of the metaball when debug=true, without resorting to the full custom function implementation demonstrated in Example 22. Rather than having just the function literal in the spec array, we use [function_literal, [sign,vnf]] instead, where sign is the sign of the metaball (-1 or 1) and vnf is the VNF of the debug-view shape.

metaballs() Example 31 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
// custom metaball function - a lobed object
function multilobe(point, size, lobes) =
   let(
        ang=atan2(point.y, point.x),
        r=norm([point.x,point.y])*(1.4+cos(lobes*ang)),
        dist=norm([point.z, r])
   ) size/dist;

// custom metaball debug VNF - n-pointed star
function lobes_debug_vnf(r, n) =
    let(nstar=zrot(180/n,p=path3d(star(n,r,r/6),0)))
       vnf_vertex_array(
         [down(0.3*r,nstar), up(0.3*r,nstar)],
         col_wrap=true, caps=true);

// show the object with debug VNF defined
lobes = 5;
size = 8;
spec = [
    IDENT,
    [ // use [func,[sign,vnf]] instead of func
        function(point) multilobe(point,size,lobes),
        [1, lobes_debug_vnf(size*2, lobes)]
    ]
];
metaballs(spec,
    bounding_box = [[-20,-20,-8],[20,20,8]],
    voxel_size=0.5, debug=true);



Function/Module: metaballs2d()

Synopsis: Creates a group of 2D metaballs (smoothly connected blobs). [Geom] [Region]

Topics: Metaballs, Contours, Path Generators (2D), Regions

See Also: contour(), metaballs()

Usage: As a module

  • metaballs2d(spec, bounding_box, pixel_size, [isovalue=], [use_centers=], [smoothing=], [exact_bounds=], [show_stats=], [show_box=], [debug=] ...) [ATTACHMENTS];

Usage: As a function

  • region = metaballs2d(spec, bounding_box, pixel_size, [isovalue=], [closed=], [use_centers=], [smoothing=], [exact_bounds=], [show_stats=]);

Description:

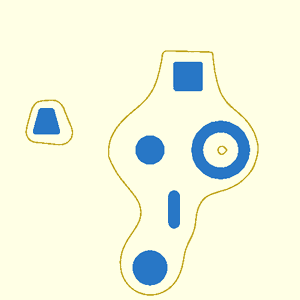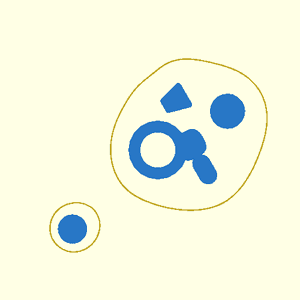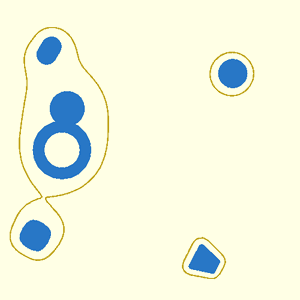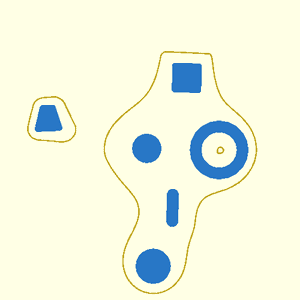
Metaball animation

2D metaball shapes can be useful to create interesting polygons for extrusion. When invoked as a module, a 2D metaball scene is displayed. When called as a function, a region or list of paths is returned.

For a full explanation of metaballs, see introduction above. The specification method, tranformations, bounding box, and other parameters are the same as in 3D, but in 2D, pixels replace voxels.

See metaball parameters for details on the primary parameters common to metaballs() and metaballs2d(). The spec parameter is described in more detail there. The spec parameter is a 1D list of alternating transforms and metaball functions; for example, the array spec= [ left(9), mb_circle(5), right(9), mb_circle(5) ] defines a scene with two circles of radius 5 shifted 9 units to the left and right of the origin. The spec parameter completely defines the metaballs in your scene, including their position, orientation, and scaling, as well as different shapes.

You can create 2D metaballs in a variety of standard shapes using the predefined functions listed below. If you wish, you can also create custom metaball shapes using your own functions. For all of the built-in 2D metaballs, three parameters are available to control the interaction of the metaballs with each other: cutoff, influence, and negative.

The cutoff parameter specifies the distance beyond which the metaball has no interaction with other balls. When you apply cutoff, a smooth suppression factor begins decreasing the interaction strength at half the cutoff distance and reduces the interaction to zero at the cutoff. Depending on the value of influence, a cutoff that ends in the middle of another ball can result in strange shapes, as shown in Example 9, with the metaball interacting on one side of the boundary and not interacting on the other side. If you scale a ball, the cutoff value is also scaled.

The influence parameter adjusts the strength of the interaction that metaball objects have with each other. If you increase influence of one metaball from its default of 1, then that metaball interacts with others at a longer range, and surrounding balls grow bigger. The metaball with larger influence can also grow bigger because it couples more strongly with other nearby balls, but it can also remain nearly unchanged while influencing others when isovalue is greater than 1. Decreasing influence has the reverse effect. Small changes in influence can have a large effect; for example, setting influence=2 dramatically increases the interactions at longer distances, and you may want to set the cutoff argument to limit the range influence. At the other exteme, small influence values can produce ridge-like artifacts or texture on the model. Example 8 demonstrates this effect. To avoid these artifacts, keep influence above about 0.5 and consider using cutoff instead of using small influence.

The negative parameter, if set to true, creates a negative metaball, which can result in hollows, dents, or reductions in size of other metaballs. Negative metaballs are never directly visible; only their effects are visible. The influence argument may also behave in ways you don't expect with a negative metaball. See Examples 16 and 17.

Built-in 2D metaball functions

Several metaballs are defined for you to use in your models. All of the built-in metaballs take positional and named parameters that specify the size of the metaball (such as height or radius). The size arguments are the same as those for the regular objects of the same type (e.g. a circle accepts both r for radius and the named parameter d= for diameter). The size parameters always specify the size of the metaball in isolation with isovalue=1. The metaballs can grow much bigger than their specified sizes when they interact with each other. Changing isovalue also changes the sizes of metaballs. They grow bigger than their specified sizes, even in isolation, if isovalue < 1 and smaller than their specified sizes if isovalue > 1.

The built-in 2D metaball functions are listed below. As usual, arguments without a trailing = can be used positionally; arguments with a trailing = must be used as named arguments.

  • mb_circle(r|d=) — circular metaball, with radius r or diameter d. You can create an ellipse using scale() as the last transformation entry of the metaball spec array.
  • mb_rect(size, [squareness=]) — a square/circle hybrid known as a squircle, appearing as a square with rounded edges and corners. The corner sharpness is controlled by the squareness parameter ranging from 0 (circular) to 1 (square), and defaults to 0.5. The size parameter specifies the dimensions of the squircle that circumscribes the rounded shape, which is tangent to the center of each square side. The size parameter may be a scalar or a vector, as in squircle(). Except when squareness=1, the sides are always a little bit curved.
  • mb_trapezoid(h, w1|w=, w2|w=, [ang=], [rounding=]) — rounded trapezoid metaball with arguments similar to trapezoid(). Any three of the arguments h (height), w1 (bottom width), w2 (top width), or ang (bottom corner angle) may be specified, and w sets both w1 and w2 to the same size. The rounding argument defaults to 0 (sharp edge) if not specified. Only one rounding value is allowed: the rounding is the same at both ends. For a rounded rectangular shape, consider using mb_rect(), or mb_stadium(), which are less flexible but have faster execution time.
  • mb_stadium(size) — rectangle with rounded caps on the narrow ends. The object is a convex hull of two circles. Set the size parameter to [width,height] to get an object that fits inside a rectangle of that size. Giving a scalar size produces a circle.
  • mb_connector2d(p1, p2, [r|d=]) — a stadium shape specified to connect point p1 to point p2 (which must be different 2D coordinates). As with mb_stadium(), the object is a convex hull of two circles. The points p1 and p2 are at the centers of the two round caps. The connectors themselves are still influenced by other metaballs, but it may be undesirable to have them influence others, or each other. If two connectors are connected, the joint may appear swollen unless influence or cutoff is reduced. Reducing cutoff is preferable if feasible, because reducing influence can produce interpolation artifacts.
  • mb_ring(r1|d1=, r2|d2=) — 2D ring metaball using a subset of ring() parameters, with inner radius being the smaller of r1 and r2, and outer radius being the larger of r1 and r2. If cutoff is applied, it is measured from the circle midway between r1 and r2.

In addition to the dimensional arguments described above, all of the built-in functions accept the following named arguments:

  • cutoff — positive value giving the distance beyond which the metaball does not interact with other balls. Cutoff is measured from the object's center. Default: INF
  • influence — a positive number specifying the strength of interaction this ball has with other balls. Default: 1
  • negative — when true, creates a negative metaball. Default: false
  • hide_debug — when true, suppresses the display of the underlying metaball shape when debug=true is set in the metaballs() module. This is useful to hide shapes that may be overlapping others in the debug view. Default: false

Closed and unclosed paths

The functional form of metaballs2d() supports a closed parameter. When closed=true (the default) and a polygon is clipped by the bounding box, the bounding box edges are included in the polygon. The resulting path list is a valid region with no duplicated vertices in any path. The module form of metaballs2d() always closes the polygons.

When closed=false, paths that intersect the edge of the bounding box end at the bounding box. This means that the list of paths may include a mixture of closed and open paths. Regardless of whether any of the output paths are open, all closed paths have identical first and last points so that closed and open paths can be distinguished. You can use are_ends_equal() to determine if a path is closed. A path list that includes open paths is not a region, because regions are lists of closed polygons. Duplicating the ends of closed paths can cause problems for functions such as offset(), which would complain about repeated points. You can pass a closed path to list_unwrap() to remove the extra endpoint.

Arguments:

By Position What it does
spec Metaball specification in the form [trans0, spec0, trans1, spec1, ...], with alternating transformation matrices and metaball specs, where spec0, spec1, etc. can be a metaball function or another metaball specification.
bounding_box The volume in which to perform computations, expressed as a scalar size of a square centered on the origin, or a pair of 2D points [[xmin,ymin], [xmax,ymax]] specifying the minimum and maximum box corner coordinates. Unless you set exact_bounds=true, the bounding box size may be enlarged to fit whole pixels.
pixel_size Size of the pixels used to sample the bounding box area, can be a scalar or 2-vector, or omitted if pixel_count is set. You may get a non-square pixels of a slightly different size than requested if exact_bounds=true.
By Name What it does
pixel_count Approximate number of pixels in the bounding box. If exact_bounds=true then the pixels may not be squares. Use with show_stats=true to see the corresponding pixel size. Default: 1024 (if pixel_size not set)
isovalue A scalar value specifying the isosurface value (threshold value) of the metaballs. At the default value of 1.0, the internal metaball functions are designd so the size arguments correspond to the size parameter (such as radius) of the metaball, when rendered in isolation with no other metaballs. You can also specify a range for isovalue, such as [1,1.1] in which case the metaball is displayed as a shell with the hollow inside corresponding to the higher isovalue. A scalar isovalue is equivalent to the vector [isovalue,INF]. Default: 1.0
closed (Function only) When true, close the path if it intersects the bounding box by adding a closing side. When false, do not add a closing side. Default: true, and always true when called as a module.
use_centers When true, uses the center value of each pixel as an additional data point to refine the contour path through the pixel. Default: false
smoothing Number of times to apply a 2-point moving average to the contours. This can remove small zig-zag artifacts resulting from a contour that follows the profile of a triangulated 3D surface when use_centers is set. Default: 2 if use_centers=true, 0 otherwise.
exact_bounds When true, shrinks pixels as needed to fit whole pixels inside the requested bounding box. When false, enlarges bounding_box as needed to fit whole pixels of pixel_size, and centers the new bounding box over the requested box. Default: false
show_stats If true, display statistics about the metaball isosurface in the console window. Besides the number of pixels that the contour passes through, and the number of segments making up the contour, this is useful for getting information about a possibly smaller bounding box to improve speed for subsequent renders. Default: false
show_box (Module only) Display the requested bounding box as a transparent rectangle. This box may appear slightly different than specified if the actual bounding box had to be expanded to accommodate whole pixels. Default: false
debug (Module only) Display the underlying primitive metaball shapes using your specified dimensional arguments, overlaid by the metaball scene rendered as outlines. Positive metaballs appear blue, negative appears orange, and any custom function with no debug polygon defined appears as a gray triangle of radius 5.
cp (Module only) Center point for determining intersection anchors or centering the shape. Determines the base of the anchor vector. Can be "centroid", "mean", "box" or a 3D point. Default: "centroid"
anchor (Module only) Translate so anchor point is at origin (0,0,0). See anchor. Default: "origin"
spin (Module only) Rotate this many degrees around the Z axis after anchor. See spin. Default: 0
orient (Module only) Vector to rotate top toward, after spin. See orient. Default: UP
atype (Module only) Select "hull" or "intersect" anchor type. Default: "hull"

Anchor Types:

Anchor Type What it is
"hull" Anchors to the virtual convex hull of the shape.
"intersect" Anchors to the surface of the shape.

Side Effects:

  • $metaball_pathlist is set to the region (array of contor paths) of the metaball scene.

Example 1: Two circles interacting.

metaballs2d() Example 1 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(9), mb_circle(5),
    right(9), mb_circle(5)
];
metaballs2d(spec, pixel_size=1,
    bounding_box=[[-16,-7], [16,7]]);



Example 2: Two rounded rectangles (squircles) interacting.

metaballs2d() Example 2 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    move([-8,-6]), mb_rect(10),
    move([8,6]), mb_rect(10)
];
metaballs2d(spec, pixel_size=1,
    bounding_box=[[-15,-13], [15,13]]);



Example 3: Two rounded trapezoids interacting.

metaballs2d() Example 3 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(10), mb_trapezoid(15, w1=12, w2=8, rounding=2),
    right(10), mb_trapezoid(15, w1=12, w2=8, rounding=2)
];
metaballs2d(spec, pixel_size=1,
    bounding_box=[[-17,-10], [17,10]]);



Example 4: Two stadiums interacting. The first stadium of size [6,16] has width less than height, which would normally be oriented vertically unless rotated 90° as done here. The second stadum of size [16,6] has width greater than height and is already oriented horizontally without rotation.

metaballs2d() Example 4 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
metaballs2d([
    move([-8,4])*zrot(90), mb_stadium([6,16]),
    move([8,-4]), mb_stadium([16,6])
    ], [[-17,-8], [17,8]], 1);



Example 5: A circle with two connectors.

metaballs2d() Example 5 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
path = [[-20,0], [0,1], [-3,-10]];
spec = [
    move(path[0]), mb_circle(6),
    for(seg=pair(path)) each
       [IDENT, mb_connector2d(seg[0],seg[1],
        2, influence=0.5)]
];
metaballs2d(spec, pixel_size=1,
    bounding_box=[[-27,-13], [4,14]]);



Example 6: Interaction between two rings.

metaballs2d() Example 6 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    move([-7,-3]), mb_ring(3,6),
    move([7,3]),   mb_ring(3,7)
];
pixel_size = 0.5;
boundingbox = [[-14,-11], [16,11]];
metaballs2d(spec, boundingbox, pixel_size);



Example 7: Setting influence to less than 0.5 can cause interpolation artifacts in the contour. The only difference between these two circles is influence. Both have cutoff set to prevent them from affecting each other. The circle on the right has a low influence of 0.02, which translates to a falloff with distance $d$ proportional to $1/d^{50}$. That high exponent increases the non-linear nature of the function gradient at the contour isovalue, reducing the accuracy of the linear interpolation of where the the contour intersects each pixel, causing bumps to appear. It is usually better to use cutoff to limit the range of influence rather than reducing influence significantly below 1.

metaballs2d() Example 7 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    left(10), mb_circle(8, cutoff=10, influence=1),
    right(10), mb_circle(8, cutoff=10, influence=0.02)
];
bbox = [[-18,-8], [18,8]];
metaballs2d(spec, bounding_box=bbox, pixel_size=0.4);

Example 8: A positive and negative metaball in close proximity, with the small negative metaball creating a dent in the large positive one. Small green cylinders indicate the center of each metaball. The negative metaball isn't visible because its field is negative; the contour encloses only field values greater than the isovalue of 1.

metaballs2d() Example 8 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
centers = [[-1,0], [1.25,0]];
spec = [
    move(centers[0]), mb_circle(8),
    move(centers[1]), mb_circle(3, negative=true)
];
voxel_size = 0.25;
boundingbox = [[-7,-6], [3,6]];
metaballs2d(spec, boundingbox, voxel_size);
color("green") move_copies(centers) cylinder(h=1,d=1,$fn=16);



Example 9: When a positive and negative metaball interact, the negative metaball reduces the influence of the positive one, causing it to shrink, but not disappear because its contribution approaches infinity at its center. This example shows a large positive metaball near a small negative metaball at the origin. The negative ball has high influence, and a cutoff limiting its influence to 20 units. The negative metaball influences the positive one up to the cutoff, causing the positive metaball to appear smaller inside the cutoff range, and appear its normal size outside the cutoff range. The positive metaball has a small dimple at the origin (the center of the negative metaball) because it cannot overcome the infinite negative contribution of the negative metaball at the origin.

metaballs2d() Example 9 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
spec = [
    back(10), mb_circle(20),
    IDENT, mb_circle(2, influence=30,
        cutoff=20, negative=true),
];
pixel_size = 0.5;
boundingbox = [[-20,-1], [20,31]];
metaballs2d(spec, boundingbox, pixel_size);



Example 10: Profile of an airplane, constructed only from metaball circles with scaling. The bounding box is used to clip the wingtips and tail.

metaballs2d() Example 10 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
bounding_box = [[-55,-50],[35,50]];
spec = [
    // fuselage
    move([-18,0])*scale([27,4]), mb_circle(1),
    // tail
    move([30,0])*scale([3,15]),  mb_circle(1),
    // wing
    move([-15,0])*scale([6,45]), mb_circle(1)
];
pixel_size = 1;
color("lightblue") zrot(-90)
  metaballs2d(spec, bounding_box, pixel_size);



Example 11: This is the 2D version of the 3D Example 20 above, showing a custom metaball defined and passed as a function literal that takes a single [x,y] argument representing a coordinate relative to the metaball center, called point here, but can have any name. This distance vector from the origin is calculated internally and always passed to the function. Inside the function, it is converted to a scalar distance dist. The function literal expression sets all of your parameters. Only point is not set, and it becomes the single parameter to the function literal. The spec argument invokes your custom function as a function literal that passes point into it.

metaballs2d() Example 11 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function threelobe2d(point) =
   let(
        ang=atan2(point.y, point.x),
        dist=norm([point.x,point.y])*(1.3+cos(3*ang))
   ) 3/dist;
metaballs2d(
    spec = [
        IDENT, function (point) threelobe2d(point),
        IDENT, mb_circle(r=3)
    ],
    bounding_box = [[-14,-12],[8,12]],
    pixel_size=0.5);



Example 12: Analogous to the 3D Example 21 above, here is a 2D function nearly identical to the previous example, introducing additional dimensional parameters into the function to control its size and number of lobes. If you expiriment with this using different argument values, you should increase the bounding box along with pixel size.

metaballs2d() Example 12 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function multilobe2d(point, size, lobes) =
   let(
        ang=atan2(point.y, point.x),
        dist = norm([point.x,point.y])
            * (1.3+cos(lobes*ang))
   ) size/dist;
metaballs2d(
    spec = [
        left(7),
           function (point) multilobe2d(point,3,4),
        right(7)*zrot(60),
           function (point) multilobe2d(point,3,3)
    ],
    bounding_box = [[-16,-13],[18,13]],
    pixel_size=0.4);



Section: Isosurfaces (3D) and contours (2D)

The isosurface of a function $f(x,y,z)$ is the set of points where $f(x,y,z)=c$ for some constant isovalue $c$.

The contour of a function $f(x,y)$ is the set of points where $f(x,y)=c$ for some constant isovalue $c$. Considered in the context of an elevation map, the function returns an elevation associated with any $(x,y)$ point, and the isovalue $c$ is a specific elevation at which to compute the contour paths. Any 2D cross-section of an isosurface is a contour.

Parameters common to isosurface() and contour()

Parameter f (function): The function literal must take 3 parameters (x, y and z) for isosurface or two parameters (x and y) for contour, and must return a single numerical value. You can also define an isosurface or contour using an array of values instead of a function, in which case the isosurface or contour is the set of points equal to the isovalue as interpolated from the array. The array indices are in the order [x][y][z] in 3D, and [x][y] in 2D.

Parameter isovalue: The isovalue must be specified as a range [c_min,c_max]. The range can be finite or unbounded at one end, with either c_min=-INF or c_max=INF. For isosurface, the returned object is the set of points [x,y,z] that satisfy c_min <= f(x,y,z) <= c_max, or in 2D, the points [x,y] satisfying c_min <= f(x,y) <= c_max. Strictly speaking, this means the isosurface and contour modules don't return a single contour or isovalue by the shape bounded by isosurfaces or contours. If the function has values larger than c_min and values smaller than c_max, then the result is a shell object (3D) or ring object (2D) with two bounding surfaces/curves corresponding to the isovalues of c_min and c_max. If the function is smaller than c_max everywhere (which is true when c_max = INF), then no isosurface exists for c_max, so the object has only one bounding surface: the one defined by c_min. This can result in a bounded object—a sphere or circle—or an unbounded object such as all the points outside of a sphere out to infinity. A similar situation arises if the function is larger than c_min everywhere (which is true when c_min = -INF). Setting isovalue to [-INF,c_max] or [c_min,INF] always produces an object with a single bounding isosurface or contour, which itself can be unbounded. To obtain a bounded object, think about whether the function values inside your object are smaller or larger than your iso value. If the values inside are smaller, you produce a bounded object using [-INF,c_max]. If the values inside are larger, you get a bounded object using [c_min,INF]. When your object is unbounded, it will be truncated at the bounded box, which can result in an object that looks like a simple cube.

Parameters bounding_box and grid units: The isosurface or contour is evaluated over a bounding box. The bounding_box parameter can be specified by its minimum and maximum corners: [[xmin,ymin,zmin],[xmax,ymax,zmax]] in 3D, or [[xmin,ymin],[xmax,ymax]] in 2D. The bounding box can also be specified as a scalar of a cube (in 3D) or square (in 2D) centered on the origin.

This bounding box is divided into grid units, specified as voxel_size in 3D or pixel_size in 2D, which can be a scalar or a vector size. Alternately, you can set the grid count (voxel_count or pixel_count) to fit approximately the specified number of grid units into the bounding box.

Features in the scene having any dimension smaller than the grid spacing may not be displayed, so if something seems to be missing, try making the grid units smaller or the grid count larger. By default, if the voxel size or pixel size doesn't exactly divide your specified bounding box, then the bounding box is enlarged to contain whole grid units, and centered on your requested box. Alternatively, you may set exact_bounds=true to cause the grid units to adjust in size to fit instead, resulting in non-square grid units.

The isosurface or contour object is clipped by the bounding box. The contour module always closes the shapes at the boundary to produce displayable polygons. The isosurface module and the function forms accept a closed parameter. Setting closed=false causes the closing segments or surfaces along the bounding box to be excluded from the model. In 3D, this results in a non-manifold shape with holes, exposing the inside of the object. In 2D, this results in an open-ended contour path with higher values on the right with respect to the path direction.

Isosurface and contour run time

The size of the voxels or pixels, and size of the bounding box affects the run time, which can be long. This is usually more noticeable in 3D than 2D. In 3D, a voxel size of 1 with a bounding box volume of 200×200×200 may be slow because it requires the calculation and storage of eight million function values, and more processing and memory to generate the triangulated mesh. On the other hand, a voxel size of 5 over a 100×100×100 bounding box requires only 8,000 function values and a modest computation time. A good rule is to keep the number of voxels below 10,000 for preview, and adjust the voxel size smaller for final rendering. If you don't specify voxel_size or voxel_count then metaballs uses a default voxel_count of 10000, which should be reasonable for initial preview. Because a bounding box that is too large wastes time computing function values that are not needed, you can also set the parameter show_stats=true to get the actual bounds of the voxels intersected by the surface. With this information, you may be able to decrease run time, or keep the same run time but increase the resolution.

Function/Module: isosurface()

Synopsis: Creates a 3D isosurface (a 3D contour) from a function or array of values. [Geom] [VNF]

Topics: Isosurfaces, VNF Generators

Usage: As a module

  • isosurface(f, isovalue, bounding_box, voxel_size, [voxel_count=], [reverse=], [closed=], [exact_bounds=], [show_stats=], ...) [ATTACHMENTS];

Usage: As a function

  • vnf = isosurface(f, isovalue, bounding_box, voxel_size, [voxel_count=], [reverse=], [closed=], [exact_bounds=], [show_stats=]);

Description:

Computes a VNF structure of an object bounded by an isosurface or a range between two isosurfaces, within a specified bounding box.

See Isosurface contour parameters for details about how the primary parameters work for isosurfaces.

Why does my object appear as a cube? If your object is unbounded, then when it intersects with the bounding box and closed=true, the result may appear to be a solid cube, because the clipping faces are all you can see and the bounding surface is hidden inside. Setting closed=false removes the bounding box faces and exposes the inside structure (with inverted faces). If you want the bounded object, you can correct this problem by changing your isovalue range. If you were using a finite range [c1,c2], try changing it to [c2,INF] or [-INF,c1]. If you were using an unbounded range like [c,INF], try switching the range to [-INF,c].

Manifold warnings: The point list in the generated VNF structure contains many duplicated points. This is normally not a problem for rendering the shape, but machine roundoff differences may result in Manifold issuing warnings when doing the final render, causing rendering to abort if you have enabled the "stop on first warning" setting. You can prevent this by passing the VNF through vnf_quantize() using a quantization of 1e-7, or you can pass the VNF structure into vnf_merge_points(), which also removes the duplicates. Additionally, flat surfaces (often resulting from clipping by the bounding box) are triangulated at the voxel size resolution, and these can be unified into a single face by passing the vnf structure to vnf_unify_faces(). These steps can be computationally expensive and are not normally necessary.

Arguments:

By Position What it does
f The isosurface function literal or array. As a function literal, x,y,z must be the first arguments.
isovalue A 2-vector giving an isovalue range. For an unbounded range, use [-INF, max_isovalue] or [min_isovalue, INF].
bounding_box The volume in which to perform computations, expressed as a scalar size of a cube centered on the origin, or a pair of 3D points [[xmin,ymin,zmin], [xmax,ymax,zmax]] specifying the minimum and maximum box corner coordinates. Unless you set exact_bounds=true, the bounding box size may be enlarged to fit whole voxels. When f is an array of values, bounding_box cannot be supplied if voxel_size is supplied because the bounding box is already implied by the array size combined with voxel_size, in which case this implied bounding box is centered around the origin.
voxel_size Size of the voxels used to sample the bounding box volume, can be a scalar or 3-vector, or omitted if voxel_count is set. You may get non-cubical voxels of a slightly different size than requested if exact_bounds=true.
By Name What it does
voxel_count Approximate number of voxels in the bounding box. If exact_bounds=true then the voxels may not be cubes. Use with show_stats=true to see the corresponding voxel size. Default: 10000 (if voxel_size not set)
closed When true, close the surface if it intersects the bounding box by adding a closing face. When false, do not add a closing face and instead produce a non-manfold VNF that has holes. Default: true
reverse When true, reverses the orientation of the VNF faces. Default: false
exact_bounds When true, shrinks voxels as needed to fit whole voxels inside the requested bounding box. When false, enlarges bounding_box as needed to fit whole voxels of voxel_size, and centers the new bounding box over the requested box. Default: false
show_stats If true, display statistics in the console window about the isosurface: number of voxels that the surface passes through, number of triangles, bounding box of the voxels, and voxel-rounded bounding box of the surface, which may help you reduce your bounding box to improve speed. Enabling this parameter has a slight speed penalty. Default: false
show_box (Module only) display the requested bounding box as transparent. This box may appear slightly different than specified if the actual bounding box had to be expanded to accommodate whole voxels. Default: false
convexity (Module only) Maximum number of times a line could intersect a wall of the shape. Affects preview only. Default: 6
cp (Module only) Center point for determining intersection anchors or centering the shape. Determines the base of the anchor vector. Can be "centroid", "mean", "box" or a 3D point. Default: "centroid"
anchor (Module only) Translate so anchor point is at origin (0,0,0). See anchor. Default: "origin"
spin (Module only) Rotate this many degrees around the Z axis after anchor. See spin. Default: 0
orient (Module only) Vector to rotate top toward, after spin. See orient. Default: UP
atype (Module only) Select "hull" or "intersect" anchor type. Default: "hull"

Anchor Types:

Anchor Type What it is
"hull" Anchors to the virtual convex hull of the shape.
"intersect" Anchors to the surface of the shape.

Named Anchors:

Anchor Name Position
"origin" Anchor at the origin, oriented UP.

Example 1: These first three examples demonstrate the effect of isovalue range for the simplest of all surfaces: a sphere where $r=\sqrt{x^2+y^2+z^2}$, or r = norm([x,y,z]) in OpenSCAD. Then, the isosurface corresponding to an isovalue of 10 is every point where the expression norm([x,y,z]) equals a radius of 10. We use the isovalue range [-INF,10] here to make the sphere, with a bounding box that cuts off half the sphere. The isovalue range could also be [0,10] because the minimum value of the expression is zero.

isosurface() Example 1 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
isovalue = [-INF,10];
bbox = [[-11,-11,-11], [0,11,11]];
isosurface(function (x,y,z) norm([x,y,z]),
   isovalue, bbox, voxel_size = 1);



Example 2: An isovalue range [8,10] gives a shell with inner radius 8 and outer radius 10.

isosurface() Example 2 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
isovalue = [8,10];
bbox = [[-11,-11,-11], [0,11,11]];
isosurface(function (x,y,z) norm([x,y,z]),
   isovalue, bbox, voxel_size = 1);



Example 3: Here we set the isovalue range to [10,INF]. Because the sphere expression norm(xyz) has larger values growing to infinity with distance from the origin, the resulting object appears as the bounding box with a radius-10 spherical hole.

isosurface() Example 3 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
isovalue = [10,INF];
bbox = [[-11,-11,-11], [0,11,11]];
isosurface(function (x,y,z) norm([x,y,z]),
   isovalue, bbox, voxel_size = 1);



Example 4: Unlike a sphere, a gyroid is unbounded; it's an isosurface defined by all the zero values of a 3D periodic function. To illustrate what the surface looks like, closed=false has been set to expose both sides of the surface. The surface is periodic and tileable along all three axis directions. This is a non-manifold surface as displayed, not useful for 3D modeling. This example also demonstrates using an additional parameter in the field function beyond just the [x,y,z] input; in this case to control the wavelength of the gyroid.

isosurface() Example 4 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function gyroid(x,y,z, wavelength) = let(
    p = 360/wavelength * [x,y,z]
) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
isovalue = [0,INF];
bbox = [[-100,-100,-100], [100,100,100]];
isosurface(function(x,y,z) gyroid(x,y,z, wavelength=200),
    isovalue, bbox, voxel_size=5, closed=false);



Example 5: If we remove the closed parameter or set it to true, the isosurface algorithm encloses the entire half-space bounded by the "inner" gyroid surface, leaving only the "outer" surface exposed. This is a manifold shape but not what we want if trying to model a gyroid.

isosurface() Example 5 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function gyroid(x,y,z, wavelength) = let(
    p = 360/wavelength * [x,y,z]
) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
isovalue = [0,INF];
bbox = [[-100,-100,-100], [100,100,100]];
isosurface(function(x,y,z) gyroid(x,y,z, wavelength=200),
    isovalue, bbox, voxel_size=5, closed=true);



Example 6: To make the gyroid a double-sided surface, we need to specify a small range around zero for isovalue. Now we have a double-sided surface although with closed=false the edges are not closed where the surface is clipped by the bounding box.

isosurface() Example 6 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function gyroid(x,y,z, wavelength) = let(
    p = 360/wavelength * [x,y,z]
) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
isovalue = [-0.3, 0.3];
bbox = [[-100,-100,-100], [100,100,100]];
isosurface(function(x,y,z) gyroid(x,y,z, wavelength=200),
    isovalue, bbox, voxel_size=5, closed=false);



Example 7: To make the gyroid a valid manifold 3D object, we remove the closed parameter (same as setting closed=true), which closes the edges where the surface is clipped by the bounding box.

isosurface() Example 7 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function gyroid(x,y,z, wavelength) = let(
    p = 360/wavelength * [x,y,z]
) sin(p.x)*cos(p.y)+sin(p.y)*cos(p.z)+sin(p.z)*cos(p.x);
isovalue = [-0.3, 0.3];
bbox = [[-100,-100,-100], [100,100,100]];
isosurface(function(x,y,z) gyroid(x,y,z, wavelength=200),
    isovalue, bbox, voxel_size=5);



Example 8: An approximation of the triply-periodic minimal surface known as Schwartz P.

isosurface() Example 8 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function schwartz_p(x,y,z, wavelength) = let(
    p = 360/wavelength,
    px = p*x, py = p*y, pz = p*z
)  cos(px) + cos(py) + cos(pz);
isovalue = [-0.2, 0.2];
bbox = [[-100,-100,-100], [100,100,100]];
isosurface(function (x,y,z) schwartz_p(x,y,z, 100),
    isovalue, bounding_box=bbox, voxel_size=4);



Example 9: Another approximation of the triply-periodic minimal surface known as Neovius.

isosurface() Example 9 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function neovius(x,y,z, wavelength) = let(
    p = 360/wavelength,
    px = p*x, py = p*y, pz = p*z
)  3*(cos(px) + cos(py) + cos(pz)) + 4*cos(px)*cos(py)*cos(pz);
bbox = [[-100,-100,-100], [100,100,100]];
isosurface(function (x,y,z) neovius(x,y,z, 200),
    isovalue = [-0.3, 0.3],
    bounding_box = bbox, voxel_size=4);

Example 10: Example of a bounded isosurface.

isosurface() Example 10 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
isosurface(
    function (x,y,z)
        let(a=xyz_to_spherical([x,y,z]),
            r=a[0],
            phi=a[1],
            theta=a[2]
        ) 1/(r*(3+cos(5*phi)+cos(4*theta))),
    isovalue = [0.1,INF],
    bounding_box = [[-8,-7,-8],[6,7,8]],
    voxel_size = 0.25);



Example 11: Another example of a bounded isosurface.

isosurface() Example 11 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
isosurface(function (x,y,z)
      2*(x^4 - 2*x*x + y^4
         - 2*y*y + z^4 - 2*z*z) + 3,
    bounding_box=3, voxel_size=0.07,
    isovalue=[-INF,0]);



Example 12: For shapes that occupy a cubical bounding box centered on the origin, you can simply specify a scalar for the size of the box.

isosurface() Example 12 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
isosurface(
    function (x,y,z) let(np=norm([x,y,z]))
       (x*y*z^3 + 19*x^2*z^2) / np^2 + np^2,
    isovalue=[-INF,35], bounding_box=12, voxel_size=0.25);



Example 13: An object that could be a sort of support pillar. Here we set show_box=true to reveal that the bounding box is slightly bigger than it needs to be. The argument show_stats=true also outputs the voxel bounding box size as a suggestion of what it should be.

isosurface() Example 13 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
isosurface(
    function (x,y,z) let(np=norm([x,y,z]))
       (x*y*z^3 - 3*x^2*z^2) / np^2 + np^2,
    isovalue=[-INF,35], bounding_box=[[-32,-32,-14],[32,32,14]],
    voxel_size = 0.8, show_box=true);

Example 14: You can specify non-cubical voxels for efficiency. This example shows the result of two identical surface functions. The figure on the left uses voxel_size=1, which washes out the detail in the z direction. The figure on the right shows the same shape with voxel_size=[0.5,1,0.2] to give a bit more resolution in the x direction and much more resolution in the z direction. This example runs about six times faster than if we used a cubical voxel of size 0.2 to capture the detail in only one axis at the expense of unnecessary detail in other axes.

isosurface() Example 14 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
function shape(x,y,z, r=5) =
    r / sqrt(x^2 + 0.5*(y^2 + z^2) + 0.5*r*cos(200*z));
bbox = [[-6,-8,0], [6,8,7]];

left(6) isosurface(function (x,y,z) shape(x,y,z),
    isovalue=[1,INF], bounding_box=bbox, voxel_size=1);

right(6) isosurface(function (x,y,z) shape(x,y,z),
    isovalue=[1,INF], bounding_box=bbox, voxel_size=[0.5,1,0.2]);

Example 15: Nonlinear functions with steep gradients between voxel corners at the isosurface value can show interpolation ridges because the surface position is approximated by a linear interpolation of a highly nonlinear function. The appearance of the artifacts depends on the combination of function, voxel size, and isovalue, and can look different in different circumstances. If your isovalue is positive, then you may be able to smooth out the artifacts by using the log of your function and the log of your isovalue range to get the same isosurface without artifacts. On the left, an isosurface around a steep nonlinear function (clipped on the left by the bounding box) exhibits severe interpolation artifacts. On the right, the log of the isosurface around the log of the function smooths it out nicely.

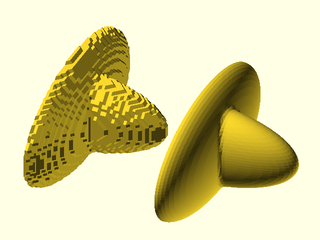
isosurface() Example 15 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
bbox = [[0,-10,-5],[9,10,6]];

function shape(x,y,z) =
        exp(-((x+5)/5-3)^2-y^2)
        *exp(-((x+5)/3)^2-y^2-z^2)
        + exp(-((y+4)/5-3)^2-x^2)
        *exp(-((y+4)/3)^2-x^2-0.5*z^2);

left(6) isosurface(function(x,y,z) shape(x,y,z),
    isovalue = [EPSILON,INF],
    bounding_box=bbox, voxel_size=0.25);
right(6) isosurface(function(x,y,z) log(shape(x,y,z)),
    isovalue = [log(EPSILON),INF],
    bounding_box=bbox, voxel_size=0.25);



Example 16: Using an array for the f argument instead of a function literal. Each row of the array represents an X index for a YZ plane with the array Z indices changing fastest in each plane. The final object may need rotation to get the orientation you want. You don't pass the bounding_box argument here; it is implied by the array size and voxel size, and centered on the origin.

isosurface() Example 16 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
field = [
  repeat(0,[6,6]),
  [ [0,1,2,2,1,0],
    [1,2,3,3,2,1],
    [2,3,4,4,3,2],
    [2,3,4,4,3,2],
    [1,2,3,3,2,1],
    [0,1,2,2,1,0]
  ],
  [ [0,0,0,0,0,0],
    [0,0,1,1,0,0],
    [0,2,3,3,2,0],
    [0,2,3,3,2,0],
    [0,0,1,1,0,0],
    [0,0,0,0,0,0]
  ],
  [ [0,0,0,0,0,0],
    [0,0,0,0,0,0],
    [0,1,2,2,1,0],
    [0,1,2,2,1,0],
    [0,0,0,0,0,0],
    [0,0,0,0,0,0]
  ],
  repeat(0,[6,6])
];
rotate([0,-90,180])
   isosurface(field, isovalue=[0.5,INF],
       voxel_size=10);



Function/Module: contour()

Synopsis: Creates a 2D contour from a function or array of values. [Geom] [Path] [Region]

Topics: Contours, Path Generators (2D), Regions

Usage: As a module

  • contour(f, isovalue, bounding_box, pixel_size, [pixel_count=], [use_centers=], [smoothing=], [exact_bounds=], [show_stats=], [show_box=], ...) [ATTACHMENTS];

Usage: As a function

  • region = contour(f, isovalue, bounding_box, pixel_size, [pixel_count=], [pc_centers=], [smoothing=], [closed=], [show_stats=]);

Description:

Computes a region that contains one or more 2D contour paths within a bounding box at a single isovalue.

See Isosurface contour parameters for details about how the primary parameters work for contours.

To provide a function, you supply a function literal taking two parameters as input to define the grid coordinate location (e.g. x,y) and returning a single numerical value. You can also define an contour using a 2D array of values (i.e. a height map) instead of a function, in which case the contour is the set of points equal to the isovalue as interpolated from the array. The array indices are in the order [x][y] with y changing fastest.

The contour is evaluated over a bounding box defined by its minimum and maximum corners, [[xmin,ymin],[xmax,ymax]]. This bounding box is divided into pixels of the specified pixel_size. Smaller pixels produce a finer, smoother result at the expense of execution time. If the pixel size doesn't exactly divide your specified bounding box, then the bounding box is enlarged to contain whole pixels, and centered on your requested box. If the bounding box clips the contour and closed=true (the default), additional edges are added along the edges of the bounds. Setting closed=false causes a clipped path to end at the bounding box.

Closed and unclosed paths

The module form of contour() always closes the polygons at the bounding box edges to produce valid polygons. The functional form of contour() supports a closed parameter. When closed=true (the default) and a polygon is clipped by the bounding box, the bounding box edges are included in the polygon. The resulting path list is a valid region with no duplicated vertices in any path.

When closed=false, paths that intersect the edge of the bounding box end at the bounding box. This means that the list of paths may include a mixture of closed and open paths. Regardless of whether any of the output paths are open, all closed paths have identical first and last points so that closed and open paths can be distinguished. You can use are_ends_equal() to determine if a path is closed. A path list that includes open paths is not a region, because regions are lists of closed polygons. Duplicating the ends of closed paths can cause problems for functions such as offset(), which will complain about repeated points or produce incorrect results. You can use list_unwrap() to remove the extra endpoint.

Arguments:

By Position What it does
f The contour function or array.
isovalue A scalar giving the isovalue for the contour, or a 2-vector giving an isovalue range (resulting in a polygon bounded by two contours). For an unbounded range, use [-INF,max_isovalue] or [min_isovalue,INF].
bounding_box The area in which to perform computations, expressed as a scalar size of a square centered on the origin, or a pair of 2D points [[xmin,ymin], [xmax,ymax]] specifying the minimum and maximum box corner coordinates. Unless you set exact_bounds=true, the bounding box size may be enlarged to fit whole pixels. When f is an array of values, bounding_box cannot be supplied if pixel_size is supplied because the bounding box is already implied by the array size combined with pixel_size, in which case this implied bounding box is centered around the origin.
pixel_size Size of the pixels used to sample the bounding box volume, can be a scalar or 2-vector, or omitted if pixel_count is set. You may get rectangular pixels of a slightly different size than requested if exact_bounds=true.
By Name What it does
pixel_count Approximate number of pixels in the bounding box. If exact_bounds=true then the pixels may not be square. Use with show_stats=true to see the corresponding pixel size. Default: 1024 (if pixel_size not set)
use_centers When true, uses the center value of each pixel as an additional data point to refine the contour path through the pixel. The center value is the function value if f is a function, or the average of the four pixel corners if f is an array. If use_centers is set to another array of center values, then those values are used. If false, the contour path doesn't account for the pixel center. Default: true
smoothing Number of times to apply a 2-point moving average to the contours. This can remove small zig-zag artifacts resulting from a contour that follows the profile of a triangulated 3D surface when use_centers is set. Default: 2 if use_centers=true, 0 otherwise.
closed (Function only) When true, close the contour path if it intersects the bounding box by adding closing edges. When false, do not add closing edges. Default: true, and always true when called as a module.
exact_bounds When true, shrinks pixels as needed to fit whole pixels inside the requested bounding box. When false, enlarges bounding_box as needed to fit whole pixels of pixel_size, and centers the new bounding box over the requested box. Default: false
show_stats If true, display statistics in the console window about the contour: number of pixels that the surface passes through, number of points in all contours, bounding box of the pixels, and pixel-rounded bounding box of the contours, which may help you reduce your bounding box to improve speed. Default: false
show_box (Module only) display the requested bounding box as a transparent rectangle. This box may appear slightly different than specified if the actual bounding box had to be expanded to accommodate whole pixels. Default: false
cp (Module only) Center point for determining intersection anchors or centering the shape. Determines the base of the anchor vector. Can be "centroid", "mean", "box" or a 3D point. Default: "centroid"
anchor (Module only) Translate so anchor point is at origin (0,0,0). See anchor. Default: "origin"
spin (Module only) Rotate this many degrees around the Z axis after anchor. See spin. Default: 0
atype (Module only) Select "hull" or "intersect" anchor type. Default: "hull"

Anchor Types:

Anchor Type What it is
"hull" Anchors to the virtual convex hull of the shape.
"intersect" Anchors to the surface of the shape.

Example 1: A small height map consisting of 8×8 data values to create a 7×7 pixel area, showing a contour at one isovalue. When passing an array as the first argument, rotating the output 90° clockwise using zrot(-90) causes the features of the contour to correspond visually to features in the array. Setting use_centers=false results in only the corner values of each pixel to be considered when drawing contour lines, resulting in coarse outlines.

contour() Example 1 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
field =[
    [0,2,2,1,0,0,0,0],
    [2,4,1,0,0,0,0,0],
    [2,2,2,1,0,0,0,0],
    [0,0,1,2,2,2,1,1],
    [0,0,2,1,0,3,1,0],
    [0,2,0,2,0,3,4,0],
    [0,0,0,1,2,3,2,0],
    [0,0,0,0,0,1,0,0]
];
isoval=[0.7,INF];
pixsize = 5;
color("lightgreen") zrot(-90)
    contour(field, isoval, pixel_size=pixsize,
        use_centers=false);
color("blue") down(1)
    square((len(field)-1)*pixsize, true);



Example 2: The same height map with the same isovalue, this time setting use_centers=true to cause the pixel center values (average of the four corners) to be considered when drawing contours, giving somewhat finer resolution. When use_centers=true, some smoothing is applied to avoid some additional crookedness in the contours that occurs due to the contours following a slice of a triangulated mesh with triangles in varying orientations.

contour() Example 2 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
field =[
    [0,2,2,1,0,0,0,0],
    [2,4,1,0,0,0,0,0],
    [2,2,2,1,0,0,0,0],
    [0,0,1,2,2,2,1,1],
    [0,0,2,1,0,3,1,0],
    [0,2,0,2,0,3,4,0],
    [0,0,0,1,2,3,2,0],
    [0,0,0,0,0,1,0,0]
];
isoval=[0.7,INF];
pixsize = 5;
color("lightgreen") zrot(-90)
    contour(field, isoval, pixel_size=pixsize,
        use_centers=true);
color("blue") down(1)
    square((len(field)-1)*pixsize, true);



Example 3: You can pass a function literal taking x,y arguments, in which case the center value of each pixel is computed in addition to the corners for somewhat greater resolution than the specified pixel size. By default, two smoothing passes are performed on the output paths when making contours from a function.

contour() Example 3 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
wavelen=42;
wave2d = function(x,y)
    40*cos(180/wavelen*norm([x,y]));
isoval=-30;
pixsize = 10;
translate([0,0,isoval]) color("green") zrot(-90)
    contour(wave2d,
        bounding_box=[[-50,-50],[50,50]],
        isovalue=[isoval,INF], pixel_size=pixsize);
%plot3d(wave2d, [-50:pixsize:50],[-50:pixsize:50],
       style="quincunx",base=5);



Example 4: Here's a simple function that produces a contour in the shape of a flower with some petals. Note that the function has smaller values inside the shape so we choose a -INF bound for the isovalue.

contour() Example 4 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
f = function (x, y, petals=5)
    sin(petals*atan2(y,x)) + norm([x,y]);
contour(f, isovalue=[-INF,3], bounding_box=8.1);



Example 5: If we instead use a +INF bound then we get the bounding box with the flower shape removed.

contour() Example 5 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
f = function (x, y, petals=5)
    sin(petals*atan2(y,x)) + norm([x,y]);
contour(f, isovalue=[3,INF], bounding_box=8.1);



Example 6: We can take the previous function a step further and make the isovalue range bounded on both ends, resulting in a hollow shell shape. The nature of the function causes the thickness to vary, which is different from the constant thickness you would get if you subtracted an offset() polygon from the inside. Here we extrude this polygon with a twist.

contour() Example 6 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
f = function (x, y, petals=5)
   sin(petals*atan2(y,x)) + norm([x,y]);
linear_extrude(6, twist=30, scale=0.75, slices=10)
   contour(f, isovalue=[2,3], bounding_box=8.1);



Example 7: Another function that needs an isovalue range to create a solid polygon. Increasing the minimum value results in holes in the object.

contour() Example 7 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
f = function(x,y) (x^2+y-11)^2 + (x+y^2-7)^2;
contour(f, bounding_box=12, isovalue=[0,125]);



Example 8: The shape of these contours are somewhat sensitive to pixel size.

contour() Example 8 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
f = function(x,y)  x^2+y^2 + 10*(1-cos(360*x)-cos(360*y));
contour(f, bounding_box=13, isovalue=[-INF,35],
    pixel_size=0.25);



Example 9: An infinite periodic pattern showing contours at one elevation in red, overlaid with a transparent render of the 3D heightmap generated by the function.

contour() Example 9 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
f = function(x,y) 100*(sin(x)*sin(y) * sin(x+y));
pixel_size = 20;
isovalue = 1;
bbox = 720;
up(isovalue) color("red") linear_extrude(1)
    contour(f, [isovalue,INF], bbox, pixel_size);
%plot3d(f, [-360:pixel_size/2:360],
        [-360:pixel_size/2:360], style="quincunx");



Example 10: A Cassini oval is a curve drawn such that for any point on the perimeter, the product of the distances from two fixed points is constant. The curve resembles two circular metaballs interacting. When the ratio b/a=1, there is a cusp where two contours meet at the origin, although the contour algorithm doesn't allow the two contours to touch.

contour() Example 10 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
a=4;  b=4.1;
f = function(x,y) (x^2+y^2)^2 - 2*a^2*(x^2-y^2) + a^4;
contour(f,bounding_box=[[-6,-3],[6,3]], isovalue=[-INF,b^4]);



Example 11: A contour of a function that looks like the contour should intersect itself at the origin, but if you zoom in, you see that it doesn't actually cross or intersect. It is theoretically possible to obtain a crossing path with contour() although the algorithm attempts to avoid it, primarily by disallowing the function values at the sample points to be equal to the specified isovalue.

contour() Example 11 
include <BOSL2/std.scad>
include <BOSL2/isosurface.scad>
g = function(x,y)
    let(
        theta=atan2(y,x),
        r = norm([x,y])
    )
    r*sin(3*theta-theta^2/20+40*r);
contour(g, bounding_box=[[-23,-13],[9,13]],
    isovalue=[0,INF], pixel_size=0.2);



Home – Table of Contents – Functions Index – Topics – Cheat Sheet – Tutorials

Indices

Table of Contents
Function Index
Topics Index
Glossary
Cheat Sheet
Tutorials

List of Files:

Basic Modeling:

Advanced Modeling:

Math:

Data Management:

Threaded Parts:

Parts:

Footnotes:

STD = Included in std.scad

Clone this wiki locally