-
|
@a-ignatieva, who has started to investigate using tree sequences to look at SARS-CoV2, pointed out a useful thing that she (and others) might want to do, which is to be able to "collapse" all the descendants of an MRCA as long as the genomes descendant from that MRCA are all clonal (i.e. have undergone no detectable recombination). This would be quite easy using An alternative requirement might be to identify ancestral nodes for which all the descendant samples are the same (i.e. there might have been recombination between the descendant lineages but not outside, defining what we might call a "monophyletic" clade in a tree sequence). I wonder if there's a nice way to identify all these nodes? |
Beta Was this translation helpful? Give feedback.
Replies: 7 comments 20 replies
-
|
Good question! I wonder is there some incremental algorithm where we work from left to right? I.e, all nodes start as clonal and then as we work through the edge_diffs we mark nodes as being non clonal if they are a parent in an edge diff, or ancestral to a parent? Must be something like that, right? |
Beta Was this translation helpful? Give feedback.
-
|
Here's another way I thought we could do it. I'm not sure if the logic is sound, though: (1) We squash edges (2) we identify all full-length edges (3) we identify all nodes which have a non-full-length descendant edge (4) we remove all edges that refer to these nodes (5) we simplify. Then (I think) the roots of any remaining trees are the clonal ancestors. I'm not sure how efficient this is, but it's nice to use existing tools. |
Beta Was this translation helpful? Give feedback.
-
|
Yes, I think that would work. We're looking for the roots of the subtrees that don't change along the full length of the sequence. |
Beta Was this translation helpful? Give feedback.
-
|
Could just delete all non-full edges, and simplify? |
Beta Was this translation helpful? Give feedback.
-
|
I thought about that, but there might be a node which has one full edge descending from it, and another half-length edge descending from it too. I don't think we could consider that node as a (uniquely) clonal ancestor? Especially if such a node is nested within an otherwise clonal tree. |
Beta Was this translation helpful? Give feedback.
-
|
We just need to ask which nodes have only one parent in the edge table, right? So, something like: I happen to have a utility for that in pyslim: |
Beta Was this translation helpful? Give feedback.
-
|
Doh, of course! Silly me. Nice one @petrelharp |
Beta Was this translation helpful? Give feedback.
-
|
Although what if a node has a single parent in the edge table, but that only spans (say) half the genome? That can happen, right? |
Beta Was this translation helpful? Give feedback.
-
|
Oh right good point. I guess we also want those that are entirely represented in the edge table, so I think this does it: |
Beta Was this translation helpful? Give feedback.
-
|
Is this the sort of thing we eventually want as a function in tskit, or is a (tested?) recipe here sufficient in this case? |
Beta Was this translation helpful? Give feedback.
-
|
I think we'd want to have a reasonably common use case and a good name for it to be worth the trouble. I'm not sure we have either yet. |
Beta Was this translation helpful? Give feedback.
-
|
Agreed. These discussion forums are a good place to template code - the only thing is that I'm not sure how we would do or store any bits of code to test solutions suggested here. |
Beta Was this translation helpful? Give feedback.
-
|
I think this does the job: import numpy as np
import msprime
ts = msprime.sim_ancestry(5,
recombination_rate=0.002, sequence_length=100, random_seed=53)
print("ORGINAL TS")
print(ts.draw_text())
tables = ts.dump_tables()
index = np.logical_and(
tables.edges.left == 0, tables.edges.right == tables.sequence_length)
tables.edges.set_columns(
left=tables.edges.left[index],
right=tables.edges.right[index],
parent=tables.edges.parent[index],
child=tables.edges.child[index])
print("ONLY FULL SPAN EDGES")
ts2 = tables.tree_sequence()
print(ts2.draw_text())
print("SIMPLIFIED (but different IDs)")
ts3, node_map = ts2.simplify(map_nodes=True)
reverse_map = {mapped: j for j, mapped in enumerate(node_map) if mapped != -1}
print(ts3.draw_text())
tree = ts3.first()
mrcas = [root for root in tree.roots]
original_nodes = [reverse_map[root] for root in mrcas]
print("TRIMMED")
ts_trimmed = ts.simplify(original_nodes)
print(ts_trimmed.draw_text())Giving: Right? Surely removing all the non-full span edges is what we want, by definition. The rest is just fiddling to get rid of some annoying topology and mapping of node IDs. |
Beta Was this translation helpful? Give feedback.
-
|
I'm not sure removing all the non-full span edges quite does it (see my comment above)? It's true that the resulting trees will all represent clonal replication, but we may have removed some sample nodes from within what was previously a tree. I think for what @a-ignatieva needs we need to also check that the resulting trees contain all the same sample nodes as in the original TS. If they don't there's some fiddling to do to find potentially appropriate clonal subtrees. I'll see if I can come up with an example, if it's not clear. |
Beta Was this translation helpful? Give feedback.
-
|
Here, for instance: import io
import tskit
nodes = io.StringIO(
"""\
id is_sample time population individual metadata
0 1 0.000000 0 -1
1 1 0.000000 0 -1
2 1 0.000000 0 -1
3 1 0.000000 0 -1
4 1 0.000000 0 -1
5 0 1.000000 0 -1
6 0 2.000000 0 -1
7 0 3.000000 0 -1
""")
edges = io.StringIO(
"""\
left right parent child
0.000000 1.000000 5 0
0.000000 1.000000 5 1
0.000000 1.000000 6 5
0.000000 1.000000 6 2
0.000000 0.500000 6 3
0.000000 1.000000 7 6
0.000000 1.000000 7 4
0.500000 1.000000 7 3
"""
)
ts = tskit.load_text(
nodes, edges, sequence_length=1, strict=False, base64_metadata=False
)
print(ts.draw_text())giving: for which the "clonal" tree is (surely?) everything below node 5. The "keep full edges" approach would create a "clonal tree" of nodes (0,1,2,4), excluding 3, and place the root at node 7. |
Beta Was this translation helpful? Give feedback.
-
|
Ah, I see, thanks @hyanwong. Nice example. Looks like we're basically in a position to give a full solution here though, putting together the various snippets above? |
Beta Was this translation helpful? Give feedback.
-
|
I think the following is the right logic for the left-to-right algorithm that @jeromekelleher suggested. Probably worth checking against @petrelharp 's suggestion? def clonal_mrcas(ts):
# full length nodes without recombination will not be a parent in the edges in or out, apart from at the start
for interval, edges_out, edges_in in ts.edge_diffs():
if interval.left==0:
is_full_length_clonal = np.ones(ts.num_nodes, dtype=bool) # all nodes start as clonal
else:
for e in edges_in:
is_full_length_clonal[e.parent] = False
for e in edges_out:
is_full_length_clonal[e.parent] = False
clonal_nodes = np.where(is_full_length_clonal)[0]
tables = ts.dump_tables()
edges = tables.edges
# only keep edges where both the child and the parent are full-length clonal nodes
keep_edge = np.logical_and(np.isin(edges.child, clonal_nodes), np.isin(edges.parent, clonal_nodes))
tables.edges.set_columns(
left = tables.edges.left[keep_edge],
right=tables.edges.right[keep_edge],
parent=tables.edges.parent[keep_edge],
child=tables.edges.child[keep_edge],
)
ts = tables.tree_sequence()
print("Debug: show the clonal subtrees", ts.draw_text(), sep="\n")
assert ts.num_trees == 1
return ts.first().rootsIt works OK on my previous example. Here's another: ts = msprime.simulate(8, recombination_rate=1, random_seed=321)
print("Original ts", ts.draw_text(), sep="\n")
clonal_nodes = clonal_mrcas(ts)
print(f"Subtrees under nodes {clonal_nodes} are clonal")
reduced_ts, node_map = ts.simplify(clonal_nodes, map_nodes=True)
print(
"The tree seq with clonal subtrees removed",
"(drawn using the original labels)",
reduced_ts.draw_text(node_labels = {n:f"{i}" for i, n in enumerate(node_map)}),
sep="\n",
)Giving |
Beta Was this translation helpful? Give feedback.
-
|
Oh, and there's a really nice way to plot the clonal subtrees in a different colour using my SVG styling. E.g. in a Jupyter notebook
|
Beta Was this translation helpful? Give feedback.
-
|
(I edited the examples above to put the "python" after the backticks in the code examples @hyanwong, so they render as Python) |
Beta Was this translation helpful? Give feedback.
-
|
Looks great @hyanwong, but can you update to get rid of the monkey patch, please? That's going to really confuse people, and it's not clear #1221 is actually the right approach. Just put in the |
Beta Was this translation helpful? Give feedback.
-
|
What do you think @a-ignatieva, does this do what you're looking for? |
Beta Was this translation helpful? Give feedback.
-
|
Yes that's perfect! Thanks! |
Beta Was this translation helpful? Give feedback.
-
|
Gah, I'm not sure the selected answer here does actually work. Here's a counterexample: tables = tskit.Tree.generate_comb(5).tree_sequence.dump_tables()
e = np.where(tables.edges.child == 2)[0][0]
tables.edges[e] = tables.edges[e].replace(right=0.5)
tables.sort()
ts = tables.tree_sequence()
print(ts.draw_text())If we run the code above, we erroneously identify the root (8) as the top of a clonal subtree: clonal_nodes = clonal_mrcas(ts)
print(f"Subtrees under nodes {clonal_nodes} are clonal")
reduced_ts, node_map = ts.simplify(clonal_nodes, map_nodes=True)
print(
"The tree seq with clonal subtrees removed",
"(drawn using the original labels)",
reduced_ts.first().draw_text(node_labels = {n:f"{i}" for i, n in enumerate(node_map)}),
sep="\n",
)The only clonal subtree here, IMO, is below node 5 (although we should also be reporting nodes 0, 1, and 2 as clonal) |
Beta Was this translation helpful? Give feedback.
-
|
I think we simply need to check that the subtrees identified by this method have the same set of samples under them in the pruned TS as in the first tree of the original TS. |
Beta Was this translation helpful? Give feedback.
-
|
Here's a more complex example, where I think the clonal subtree nodes should be defined as 8, 9, 5, and 6: tables = tskit.Tree.generate_balanced(7).tree_sequence.dump_tables()
e = np.where(tables.edges.child == 5)[0][0]
tables.edges[e] = tables.edges[e].replace(right=0.5)
tables.sort()
ts = tables.tree_sequence()
print(ts.draw_text()) |
Beta Was this translation helpful? Give feedback.
-
|
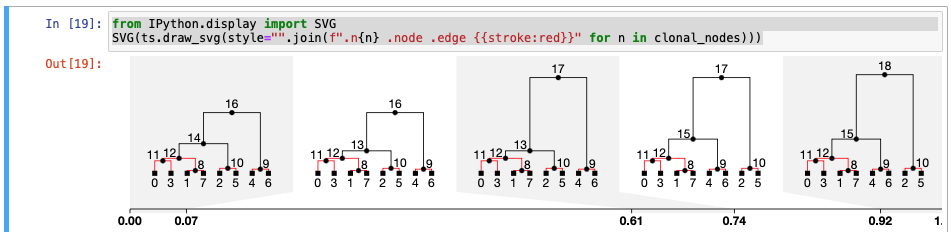
An updated answer based on my previous comments. It's more complicated because we need to follow up the trail from existing non-clonal edges and mark all their ancestors as non-clonal too. import numpy as np
def clonal_mrcas(ts, most_recent=True):
"""
Identify the nodes in a tree sequence which define clonal subtrees (i.e. in which the
samples descending from that node are identical and show identical relationships
to each other over the entire tree sequence). This includes, at its limit, nodes
with only a single descendant sample.
:param bool most_recent: If True, and the clonal node is a unary node, return IDs of the
most recent node that defines the clonal subtree. In this case, the returned IDs represent
cases where the node is either a tip or a coalescent point.
:return: a list of nodes defining subtrees which are constant over the entire tree sequence
:rtype: list
"""
for interval, edges_out, edges_in in ts.edge_diffs():
if interval.left==0:
is_full_length_clonal = np.ones(ts.num_nodes, dtype=bool) # all nodes start as clonal
else:
for e in edges_in:
is_full_length_clonal[e.parent] = False
for e in edges_out:
is_full_length_clonal[e.parent] = False
clonal_nodes = np.where(is_full_length_clonal)[0]
tables = ts.dump_tables()
edges = tables.edges
# only keep edges where both the child and the parent are full-length clonal nodes
keep_edge = np.logical_and(np.isin(edges.child, clonal_nodes), np.isin(edges.parent, clonal_nodes))
tables.edges.set_columns(
left = tables.edges.left[keep_edge],
right=tables.edges.right[keep_edge],
parent=tables.edges.parent[keep_edge],
child=tables.edges.child[keep_edge],
)
clonal_ts = tables.tree_sequence()
assert clonal_ts.num_trees == 1
# Also remove all the edges ascending from removed edges
tree = clonal_ts.first()
non_clonal_ancestors = set()
deleted_edges = np.logical_not(keep_edge)
for u in np.unique(ts.edges_parent[deleted_edges]):
while u != tskit.NULL and u not in non_clonal_ancestors:
non_clonal_ancestors.add(u)
u = tree.parent(u)
non_clonal_ancestors = np.array(list(non_clonal_ancestors))
tables = clonal_ts.dump_tables()
remove_edge = np.isin(tables.edges.parent, non_clonal_ancestors)
tables.edges.replace_with(tables.edges[np.logical_not(remove_edge)])
clonal_ts = tables.tree_sequence()
tree = ts.first(sample_lists=True)
clonal_tree = clonal_ts.first(sample_lists=True)
clonal_nodes = []
for root in clonal_tree.roots:
# Clonal trees should have the same set of samples underneath as in the original tree
assert set(tree.samples(root)) == set(clonal_tree.samples(root))
u = root
if most_recent:
# decend to the first coalescent node (i.e. MRCA)
while clonal_tree.num_children(u) == 1:
u = clonal_tree.children(u)[0]
clonal_nodes.append(u)
return clonal_nodes |
Beta Was this translation helpful? Give feedback.
-
|
Here's a demo on some of the previous examples: tables = tskit.Tree.generate_balanced(7).tree_sequence.dump_tables()
e = np.where(tables.edges.child == 5)[0][0]
tables.edges[e] = tables.edges[e].replace(right=0.5)
tables.sort()
ts = tables.tree_sequence()
print(ts.draw_text())
clonal_nodes = clonal_mrcas(ts)
print(f"Subtrees under nodes {clonal_nodes} are clonal")
reduced_ts, node_map = ts.simplify(clonal_nodes, map_nodes=True)
print(
"The tree seq with clonal subtrees removed",
"(drawn using the original labels)",
reduced_ts.draw_text(node_labels = {n:f"{i}" for i, n in enumerate(node_map)}),
sep="\n",
)Another small example import io
import tskit
nodes = io.StringIO(
"""\
id is_sample time population individual metadata
0 1 0.000000 0 -1
1 1 0.000000 0 -1
2 1 0.000000 0 -1
3 1 0.000000 0 -1
4 1 0.000000 0 -1
5 0 1.000000 0 -1
6 0 2.000000 0 -1
7 0 3.000000 0 -1
""")
edges = io.StringIO(
"""\
left right parent child
0.000000 1.000000 5 0
0.000000 1.000000 5 1
0.000000 1.000000 6 5
0.000000 1.000000 6 2
0.000000 0.500000 6 3
0.000000 1.000000 7 6
0.000000 1.000000 7 4
0.500000 1.000000 7 3
"""
)
ts = tskit.load_text(
nodes, edges, sequence_length=1, strict=False, base64_metadata=False
)
print(ts.draw_text())
clonal_nodes = clonal_mrcas(ts)
print(f"Subtrees under nodes {clonal_nodes} are clonal")
reduced_ts, node_map = ts.simplify(clonal_nodes, map_nodes=True)
print(
"The tree seq with clonal subtrees removed",
"(drawn using the original labels)",
reduced_ts.draw_text(node_labels = {n:f"{i}" for i, n in enumerate(node_map)}),
sep="\n",
)And a larger one: ts = msprime.sim_ancestry(5,
recombination_rate=0.002, sequence_length=100, random_seed=53)
print("Original ts", ts.draw_text(), sep="\n")
clonal_nodes = clonal_mrcas(ts)
print(f"Subtrees under nodes {clonal_nodes} are clonal")
reduced_ts, node_map = ts.simplify(clonal_nodes, map_nodes=True)
print(
"The tree seq with clonal subtrees removed",
"(drawn using the original labels)",
reduced_ts.draw_text(node_labels = {n:f"{i}" for i, n in enumerate(node_map)}),
sep="\n",
) |
Beta Was this translation helpful? Give feedback.
An updated answer based on my previous comments. It's more complicated because we need to follow up the trail from existing non-clonal edges and mark all their ancestors as non-clonal too.