diff --git a/README.md b/README.md
index af815c05..e8be7296 100644
--- a/README.md
+++ b/README.md
@@ -69,137 +69,21 @@ Plans for the repository can be seen in the [Issues](https://github.com/pymc-lab
Click on the thumbnail below to watch a video about CausalPy on YouTube.
[](https://www.youtube.com/watch?v=gV6wzTk3o1U)
-## Overview of package capabilities
-
-### Synthetic control
-This is appropriate when you have multiple units, one of which is treated. You build a synthetic control as a weighted combination of the untreated units.
-
-| Time | Outcome | Control 1 | Control 2 | Control 3 |
-|------|-----------|-----------|-----------|-----------|
-| 0 | $y_0$ | $x_{1,0}$ | $x_{2,0}$ | $x_{3,0}$ |
-| 1 | $y_1$ | $x_{1,1}$ | $x_{2,1}$ | $x_{3,1}$ |
-|$\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ |
-| T | $y_T$ | $x_{1,T}$ | $x_{2,T}$ | $x_{3,T}$ |
-
-
-| Frequentist | Bayesian |
-|--|--|
-|  |  |
-
-> The data (treated and untreated units), pre-treatment model fit, and counterfactual (i.e. the synthetic control) are plotted (top). The causal impact is shown as a blue shaded region. The Bayesian analysis shows shaded Bayesian credible regions of the model fit and counterfactual. Also shown is the causal impact (middle) and cumulative causal impact (bottom).
-
-### Geographical lift (Geolift)
-We can also use synthetic control methods to analyse data from geographical lift studies. For example, we can try to evaluate the causal impact of an intervention (e.g. a marketing campaign) run in one geographical area by using control geographical areas which are similar to the intervention area but which did not receive the specific marketing intervention.
-
-### ANCOVA
-
-This is appropriate for non-equivalent group designs when you have a single pre and post intervention measurement and have a treament and a control group.
-
-| Group | pre | post |
-|------|---|-------|
-| 0 | $x_1$ | $y_1$ |
-| 0 | $x_2$ | $y_2$ |
-| 1 | $x_3$ | $y_3$ |
-| 1 | $x_4$ | $y_4$ |
-
-| Frequentist | Bayesian |
-|--|--|
-| coming soon |  |
-
-> The data from the control and treatment group are plotted, along with posterior predictive 94% credible intervals. The lower panel shows the estimated treatment effect.
-
-### Difference in Differences
-
-This is appropriate for non-equivalent group designs when you have pre and post intervention measurement and have a treament and a control group. Unlike the ANCOVA approach, difference in differences is appropriate when there are multiple pre and/or post treatment measurements.
-
-Data is expected to be in the following form. Shown are just two units - one in the treated group (`group=1`) and one in the untreated group (`group=0`), but there can of course be multiple units per group. This is panel data (also known as repeated measures) where each unit is measured at 2 time points.
-
-| Unit | Time | Group | Outcome |
-|------|---|-------|-----------|
-| 0 | 0 | 0 | $y_{0,0}$ |
-| 0 | 1 | 0 | $y_{0,0}$ |
-| 1 | 0 | 1 | $y_{1,0}$ |
-| 1 | 1 | 1 | $y_{1,1}$ |
-
-| Frequentist | Bayesian |
-|--|--|
-|  |  |
-
->The data, model fit, and counterfactual are plotted. Frequentist model fits result in points estimates, but the Bayesian analysis results in posterior distributions, represented by the violin plots. The causal impact is the difference between the counterfactual prediction (treated group, post treatment) and the observed values for the treated group, post treatment.
-
-### Regression discontinuity designs
-
-Regression discontinuity designs are used when treatment is applied to units according to a cutoff on the running variable (e.g. $x$) which is typically _not_ time. By looking for the presence of a discontinuity at the precise point of the treatment cutoff then we can make causal claims about the potential impact of the treatment.
-
-| Running variable | Outcome | Treated |
-|-----------|-----------|----------|
-| $x_0$ | $y_0$ | False |
-| $x_1$ | $y_0$ | False |
-| $\ldots$ | $\ldots$ | $\ldots$ |
-| $x_{N-1}$ | $y_{N-1}$ | True |
-| $x_N$ | $y_N$ | True |
-
-
-| Frequentist | Bayesian |
-|--|--|
-|  |  |
-
-> The data, model fit, and counterfactual are plotted (top). Frequentist analysis shows the causal impact with the blue shaded region, but this is not shown in the Bayesian analysis to avoid a cluttered chart. Instead, the Bayesian analysis shows shaded Bayesian credible regions of the model fits. The Frequentist analysis visualises the point estimate of the causal impact, but the Bayesian analysis also plots the posterior distribution of the regression discontinuity effect (bottom).
-
-### Regression kink designs
-
-Regression discontinuity designs are used when treatment is applied to units according to a cutoff on a running variable, which is typically not time. By looking for the presence of a discontinuity at the precise point of the treatment cutoff then we can make causal claims about the potential impact of the treatment.
-
-| Running variable | Outcome |
-|-----------|-----------|
-| $x_0$ | $y_0$ |
-| $x_1$ | $y_0$ |
-| $\ldots$ | $\ldots$ |
-| $x_{N-1}$ | $y_{N-1}$ |
-| $x_N$ | $y_N$ |
-
-
-| Frequentist | Bayesian |
-|--|--|
-| coming soon |  |
-
-> The data and model fit. The Bayesian analysis shows the posterior mean with credible intervals (shaded regions). We also report the Bayesian $R^2$ on the data along with the posterior mean and credible intervals of the change in gradient at the kink point.
-
-### Interrupted time series
-
-Interrupted time series analysis is appropriate when you have a time series of observations which undergo treatment at a particular point in time. This kind of analysis has no control group and looks for the presence of a change in the outcome measure at or soon after the treatment time. Multiple predictors can be included.
-
-| Time | Outcome | Treated | Predictor |
-|-----------|-----------|----------|----------|
-| $t_0$ | $y_0$ | False | $x_0$ |
-| $t_1$ | $y_0$ | False | $x_1$ |
-| $\ldots$ | $\ldots$ | $\ldots$ | $\ldots$ |
-| $t_{N-1}$ | $y_{N-1}$ | True | $x_{N-1}$ |
-| $t_N$ | $y_N$ | True | $x_N$ |
-
-
-| Frequentist | Bayesian |
-|--|--|
-|  |  |
-
-> The data, pre-treatment model fit, and counterfactual are plotted (top). The causal impact is shown as a blue shaded region. The Bayesian analysis shows shaded Bayesian credible regions of the model fit and counterfactual. Also shown is the causal impact (middle) and cumulative causal impact (bottom).
-
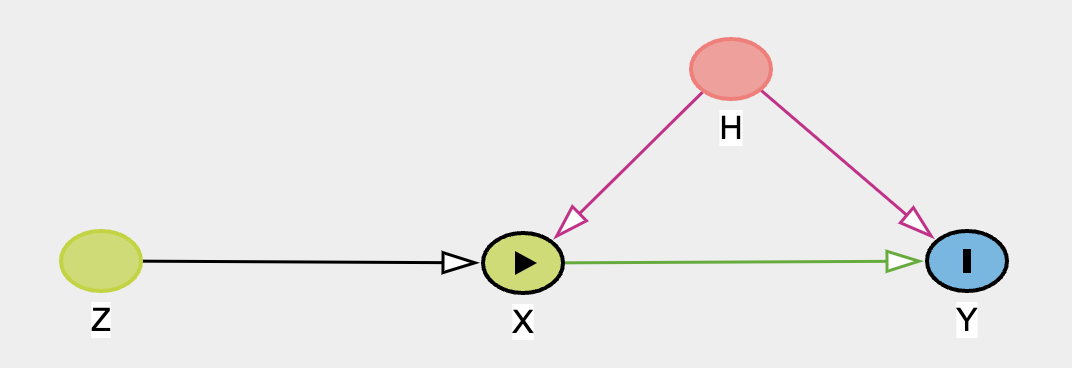
-### Instrumental Variable Regression
-
-Instrumental Variable regression is an appropriate technique when you wish to estimate the treatment effect of some variable on another, but are concerned that the treatment variable is endogenous in the system of interest i.e. correlated with the errors. In this case an “instrument” variable can be used in a regression context to disentangle treatment effect due to the threat of confounding due to endogeneity.
-
-
-
-
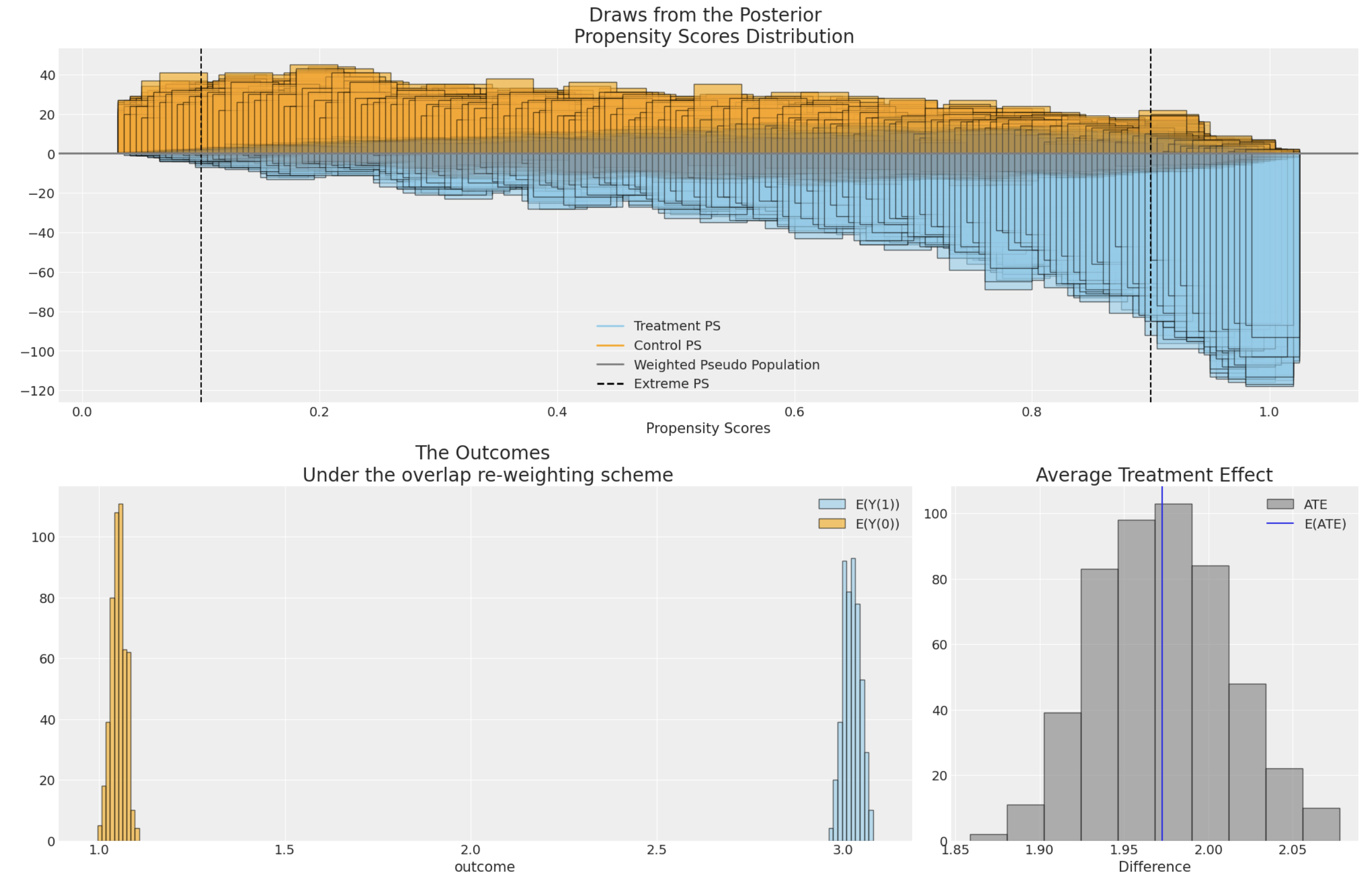
-### Inverse Propensity Score Weighting
-
-Propensity scores are often used to address the risks of bias or confounding introduced in an observational study by
-selection effects into the treatment condition. Propensity scores can be used in a number of ways, but here we demonstrate
-their usage within corrective weighting schemes aimed to recover as-if random allocation of subjects to the treatment condition.
-The technique "up-weights" or "down-weights" individual observations to better estimate a causal estimand such as the average treatment
-effect.
-
-
+## Features
+
+CausalPy has a broad range of quasi-experimental methods for causal inference:
+
+| Method | Description |
+|-|-|
+| Synthetic control | Constructs a synthetic version of the treatment group from a weighted combination of control units. Used for causal inference in comparative case studies when a single unit is treated, and there are multiple control units.|
+| Geographical lift | Measures the impact of an intervention in a specific geographic area by comparing it to similar areas without the intervention. Commonly used in marketing to assess regional campaigns. |
+| ANCOVA | Analysis of Covariance combines ANOVA and regression to control for the effects of one or more quantitative covariates. Used when comparing group means while controlling for other variables. |
+| Differences in Differences | Compares the changes in outcomes over time between a treatment group and a control group. Used in observational studies to estimate causal effects by accounting for time trends. |
+| Regression discontinuity | Identifies causal effects by exploiting a cutoff or threshold in an assignment variable. Used when treatment is assigned based on a threshold value of an observed variable, allowing comparison just above and below the cutoff. |
+| Regression kink designs | Focuses on changes in the slope (kinks) of the relationship between variables rather than jumps at cutoff points. Used to identify causal effects when treatment intensity changes at a threshold. |
+| Interrupted time series | Analyzes the effect of an intervention by comparing time series data before and after the intervention. Used when data is collected over time and an intervention occurs at a known point, allowing assessment of changes in level or trend. |
+| Instrumental variable regression | Addresses endogeneity by using an instrument variable that is correlated with the endogenous explanatory variable but uncorrelated with the error term. Used when explanatory variables are correlated with the error term, providing consistent estimates of causal effects. |
+| Inverse Propensity Score Weighting | Weights observations by the inverse of the probability of receiving the treatment. Used in causal inference to create a synthetic sample where the treatment assignment is independent of measured covariates, helping to adjust for confounding variables in observational studies. |
## Learning resources
diff --git a/docs/source/_static/anova_pymc.svg b/docs/source/_static/anova_pymc.svg
deleted file mode 100644
index e37eef86..00000000
--- a/docs/source/_static/anova_pymc.svg
+++ /dev/null
@@ -1,4362 +0,0 @@
-
-
-
diff --git a/docs/source/_static/difference_in_differences_pymc.svg b/docs/source/_static/difference_in_differences_pymc.svg
deleted file mode 100644
index 9f2cee19..00000000
--- a/docs/source/_static/difference_in_differences_pymc.svg
+++ /dev/null
@@ -1,1501 +0,0 @@
-
-
-
diff --git a/docs/source/_static/difference_in_differences_skl.svg b/docs/source/_static/difference_in_differences_skl.svg
deleted file mode 100644
index 84d8e816..00000000
--- a/docs/source/_static/difference_in_differences_skl.svg
+++ /dev/null
@@ -1,1174 +0,0 @@
-
-
-
diff --git a/docs/source/_static/interrupted_time_series_pymc.svg b/docs/source/_static/interrupted_time_series_pymc.svg
deleted file mode 100644
index cd3b21fc..00000000
--- a/docs/source/_static/interrupted_time_series_pymc.svg
+++ /dev/null
@@ -1,4333 +0,0 @@
-
-
-
diff --git a/docs/source/_static/interrupted_time_series_skl.svg b/docs/source/_static/interrupted_time_series_skl.svg
deleted file mode 100644
index 3465e62e..00000000
--- a/docs/source/_static/interrupted_time_series_skl.svg
+++ /dev/null
@@ -1,32 +0,0 @@
-
-
-
diff --git a/docs/source/_static/propensity_weight.png b/docs/source/_static/propensity_weight.png
deleted file mode 100644
index ee42d8f2..00000000
Binary files a/docs/source/_static/propensity_weight.png and /dev/null differ
diff --git a/docs/source/_static/regression_discontinuity_pymc.svg b/docs/source/_static/regression_discontinuity_pymc.svg
deleted file mode 100644
index 95d34130..00000000
--- a/docs/source/_static/regression_discontinuity_pymc.svg
+++ /dev/null
@@ -1,2204 +0,0 @@
-
-
-
diff --git a/docs/source/_static/regression_discontinuity_skl.svg b/docs/source/_static/regression_discontinuity_skl.svg
deleted file mode 100644
index fdc8476d..00000000
--- a/docs/source/_static/regression_discontinuity_skl.svg
+++ /dev/null
@@ -1,1297 +0,0 @@
-
-
-
diff --git a/docs/source/_static/regression_kink_pymc.svg b/docs/source/_static/regression_kink_pymc.svg
deleted file mode 100644
index 79c6653b..00000000
--- a/docs/source/_static/regression_kink_pymc.svg
+++ /dev/null
@@ -1,1913 +0,0 @@
-
-
-
diff --git a/docs/source/_static/synthetic_control_pymc.svg b/docs/source/_static/synthetic_control_pymc.svg
deleted file mode 100644
index f7cd50c3..00000000
--- a/docs/source/_static/synthetic_control_pymc.svg
+++ /dev/null
@@ -1,3906 +0,0 @@
-
-
-
diff --git a/docs/source/_static/synthetic_control_skl.svg b/docs/source/_static/synthetic_control_skl.svg
deleted file mode 100644
index 25262f8b..00000000
--- a/docs/source/_static/synthetic_control_skl.svg
+++ /dev/null
@@ -1,2619 +0,0 @@
-
-
-
diff --git a/docs/source/index.md b/docs/source/index.md
index 14e7960f..72025511 100644
--- a/docs/source/index.md
+++ b/docs/source/index.md
@@ -88,56 +88,19 @@ Alternatively, if you want the very latest version of the package you can instal
## Features
-
-Rather than focussing on one particular quasi-experimental setting, this package aims to have broad applicability. We can analyse data from the following quasi-experimental methods:
-
-### Synthetic control
-
-This is appropriate when you have multiple units, one of which is treated. You build a synthetic control as a weighted combination of the untreated units.
-
-
-
-### Geographical Lift / Geolift
-We can also use synthetic control methods to analyse data from geographical lift studies. For example, we can try to evaluate the causal impact of an intervention (e.g. a marketing campaign) run in one geographical area by using control geographical areas which are similar to the intervention area but which did not receive the specific marketing intervention.
-
-### ANCOVA
-
-This is appropriate when you have a single pre and post intervention measurement and have a treament and a control group.
-
-
-
-### Difference in differences
-
-This is appropriate when you have pre and post intervention measurement(s) and have a treament and a control group.
-
-
-
-### Regression discontinuity
-
-Regression discontinuity designs are used when treatment is applied to units according to a cutoff on a running variable, which is typically not time. By looking for the presence of a discontinuity at the precise point of the treatment cutoff then we can make causal claims about the potential impact of the treatment.
-
-
-
-### Regression kink designs
-
-Regression kink designs are used when there is a change in the level of treatment at a "kink point" on a running variable, which is typically not time. By looking for the presence of a discontinuity in the gradient at the kink point then we can make causal claims about the potential impact of changes in the treatment.
-
-
-
-### Interrupted time series
-Interrupted time series analysis is appropriate when you have a time series of observations which undergo treatment at a particular point in time. This kind of analysis has no control group and looks for the presence of a change in the outcome measure at or soon after the treatment time.
-
-
-
-### Instrumental Variable Regression
-Instrumental Variable regression is an appropriate technique when you wish to estimate the treatment effect of some variable on another, but are concerned that the treatment variable is endogenous in the system of interest i.e. correlated with the errors. In this case an "instrument" variable can be used in a regression context to disentangle treatment effect due to the threat of confounding due to endogeneity.
-
-
-
-### Inverse Propensity Score Weighting
-Inverse Propensity Score Weighting is a technique used to correct selection effects in observational data by re-weighting observations to better reflect an as-if random allocation to treatment status. This helps recover unbiased causal effect estimates.
-
-
+CausalPy has a broad range of quasi-experimental methods for causal inference:
+
+| Method | Description |
+|-|-|
+| Synthetic control | Constructs a synthetic version of the treatment group from a weighted combination of control units. Used for causal inference in comparative case studies when a single unit is treated, and there are multiple control units.|
+| Geographical lift | Measures the impact of an intervention in a specific geographic area by comparing it to similar areas without the intervention. Commonly used in marketing to assess regional campaigns. |
+| ANCOVA | Analysis of Covariance combines ANOVA and regression to control for the effects of one or more quantitative covariates. Used when comparing group means while controlling for other variables. |
+| Differences in Differences | Compares the changes in outcomes over time between a treatment group and a control group. Used in observational studies to estimate causal effects by accounting for time trends. |
+| Regression discontinuity | Identifies causal effects by exploiting a cutoff or threshold in an assignment variable. Used when treatment is assigned based on a threshold value of an observed variable, allowing comparison just above and below the cutoff. |
+| Regression kink designs | Focuses on changes in the slope (kinks) of the relationship between variables rather than jumps at cutoff points. Used to identify causal effects when treatment intensity changes at a threshold. |
+| Interrupted time series | Analyzes the effect of an intervention by comparing time series data before and after the intervention. Used when data is collected over time and an intervention occurs at a known point, allowing assessment of changes in level or trend. |
+| Instrumental variable regression | Addresses endogeneity by using an instrument variable that is correlated with the endogenous explanatory variable but uncorrelated with the error term. Used when explanatory variables are correlated with the error term, providing consistent estimates of causal effects. |
+| Inverse Propensity Score Weighting | Weights observations by the inverse of the probability of receiving the treatment. Used in causal inference to create a synthetic sample where the treatment assignment is independent of measured covariates, helping to adjust for confounding variables in observational studies. |
## Support
diff --git a/docs/source/notebooks/generate_plots.ipynb b/docs/source/notebooks/generate_plots.ipynb
deleted file mode 100644
index 1ddf4a4b..00000000
--- a/docs/source/notebooks/generate_plots.ipynb
+++ /dev/null
@@ -1,1054 +0,0 @@
-{
- "cells": [
- {
- "attachments": {},
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "# Generate plots for README"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 1,
- "metadata": {},
- "outputs": [],
- "source": [
- "import matplotlib.pyplot as plt\n",
- "import numpy as np\n",
- "import pandas as pd\n",
- "\n",
- "import causalpy as cp\n",
- "from causalpy.skl_models import LinearRegression"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 2,
- "metadata": {},
- "outputs": [],
- "source": [
- "seed = 42\n",
- "rng = np.random.default_rng(seed)\n",
- "image_path = \"../_static/\""
- ]
- },
- {
- "attachments": {},
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "## ANCOVA"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 3,
- "metadata": {},
- "outputs": [],
- "source": [
- "df = cp.load_data(\"anova1\")"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {},
- "source": [
- "### PyMC version"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": 4,
- "metadata": {},
- "outputs": [
- {
- "name": "stderr",
- "output_type": "stream",
- "text": [
- "Auto-assigning NUTS sampler...\n",
- "Initializing NUTS using jitter+adapt_diag...\n",
- "Multiprocess sampling (4 chains in 4 jobs)\n",
- "NUTS: [beta, sigma]\n"
- ]
- },
- {
- "data": {
- "text/html": [
- "\n",
- "\n"
- ],
- "text/plain": [
- ""
- ]
- },
- "metadata": {},
- "output_type": "display_data"
- },
- {
- "data": {
- "text/html": [
- "\n",
- "