2463. Minimum Total Distance Traveled

[mah-shamim]

Topics: Array, Dynamic Programming, Sorting

There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.

The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.

All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.

At any moment, you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.

Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.

Note that

• All robots move at the same speed.
• If two robots move in the same direction, they will never collide.
• If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
• If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
• If the robot moved from a position x to a position y, the distance it moved is |y - x|.

Example 1:

• Input: robot = [0,4,6], factory = [[2,2],[6,2]]
• Output: 4
• Explanation: As shown in the figure:
  • The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
  • The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
  • The third robot at position 6 will be repaired at the second factory. It does not need to move.
  • The limit of the first factory is 2, and it fixed 2 robots.
  • The limit of the second factory is 2, and it fixed 1 robot.
  • The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.

Example 2:

• Input: robot = [1,-1], factory = [[-2,1],[2,1]]
• Output: 2
• Explanation: As shown in the figure:
  • The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
  • The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
  • The limit of the first factory is 1, and it fixed 1 robot.
  • The limit of the second factory is 1, and it fixed 1 robot.
  • The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.

Constraints:

• 1 <= robot.length, factory.length <= 100
• factory[j].length == 2
• -109 <= robot[i], positionj <= 109
• 0 <= limitj <= robot.length
• The input will be generated such that it is always possible to repair every robot.

Hint:

1. Sort robots and factories by their positions.
2. After sorting, notice that each factory should repair some subsegment of robots.
3. Find the minimum total distance to repair first i robots with first j factories.

[mah-shamim]

We can use dynamic programming with sorted robot and factory arrays. The idea is to minimize the distance each robot must travel to be repaired by a factory, respecting each factory’s repair capacity. Here’s a step-by-step breakdown of the approach:

1. Sort the robot and factory arrays by position. Sorting helps in minimizing the travel distance as we can assign nearby robots to nearby factories.

2. Dynamic Programming Approach: We define a 2D DP table dp[i][j] where:

   • i represents the first i robots.
   • j represents the first j factories.
   • dp[i][j] stores the minimum total distance for repairing these i robots using these j factories.

3. State Transition:

   • For each factory, try to repair a subset of consecutive robots within its limit.
   • For a factory j at position p, calculate the minimum distance required for assigning k robots to it by summing the distances from each robot to the factory's position.
   • Update the DP state by selecting the minimum between repairing fewer robots or utilizing the factory capacity to the fullest.

Let's implement this solution in PHP: 2463. Minimum Total Distance Traveled

<?php
/**
 * @param Integer[] $robot
 * @param Integer[][] $factory
 * @return Integer
 */
function minimumTotalDistance($robot, $factory) {
    sort($robot);
    usort($factory, function($a, $b) {
        return $a[0] - $b[0];
    });

    $n = count($robot);
    $m = count($factory);
    $dp = array_fill(0, $n + 1, array_fill(0, $m + 1, PHP_INT_MAX));
    $dp[0][0] = 0;

    for ($j = 1; $j <= $m; $j++) {
        $pos = $factory[$j - 1][0];
        $limit = $factory[$j - 1][1];
        for ($i = 0; $i <= $n; $i++) {
            $dp[$i][$j] = $dp[$i][$j - 1];
            $sumDist = 0;
            for ($k = 1; $k <= min($limit, $i); $k++) {
                $sumDist += abs($robot[$i - $k] - $pos);
                $dp[$i][$j] = min($dp[$i][$j], $dp[$i - $k][$j - 1] + $sumDist);
            }
        }
    }

    return $dp[$n][$m];
}

// Test cases
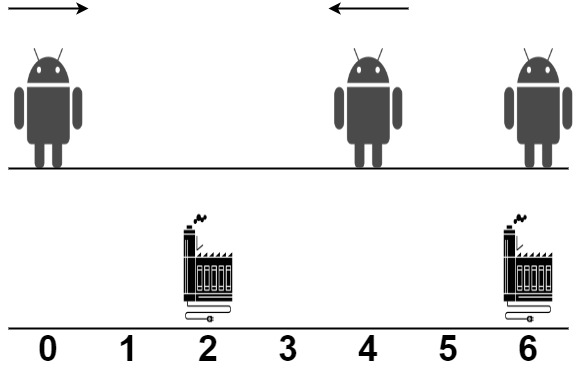
$robot = [0, 4, 6];
$factory = [[2, 2], [6, 2]];
echo minimumTotalDistance($robot, $factory);  // Output: 4

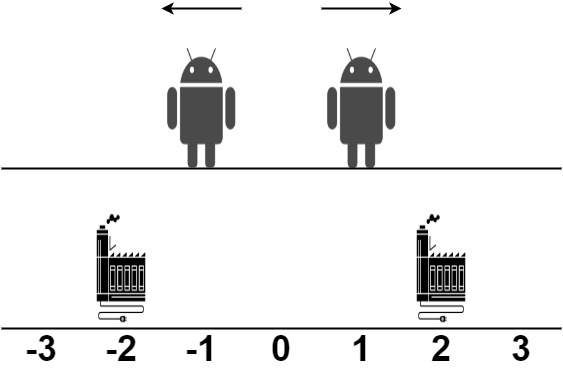
$robot = [1, -1];
$factory = [[-2, 1], [2, 1]];
echo minimumTotalDistance($robot, $factory);  // Output: 2
?>

Explanation:

• Sorting: We sort robot and factory by positions to ensure we assign nearby robots to nearby factories.
• DP Initialization: Initialize dp[0][0] = 0 since no robots repaired by no factories means zero distance.
• Dynamic Programming Transition:
  • For each factory j, we try repairing the k robots preceding it within its limit.
  • The total distance is accumulated in sumDist.
  • We update dp[i][j] with the minimum value after repairing k robots, considering the distance and previous states.

Complexity

• Time Complexity: O(n * m * L) where n is the number of robots, m is the number of factories, and L is the maximum limit of repairs any factory can handle.
• Space Complexity: O(n * m) for the DP table.

This solution efficiently calculates the minimum travel distance for all robots to be repaired within their factory limits.

[kovatz]

Thanks to solve this problem

[topugit]

Thanks

[mah-shamim]

Thanks