You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
{{ message }}
This repository was archived by the owner on Mar 24, 2022. It is now read-only.
Copy file name to clipboardExpand all lines: RSA-encryption/Attack-Franklin-Reiter/README.md
+6-6Lines changed: 6 additions & 6 deletions
Display the source diff
Display the rich diff
Original file line number
Diff line number
Diff line change
@@ -7,18 +7,18 @@ Prerequisites:
7
7
This attack works in a scenario where two messages differ only by a fixed known difference and are encrypted using public key e and same modulus N. The attacker can then recover the two messages in the above scenario using Franklin Reiter's Attack.
8
8
9
9
## Theorem
10
-
Suppose there are two messages M<sub>1</sub> and M<sub>2</sub> where M<sub>1</sub> != M<sub>2</sub>, both less than N and related to each other as {\pmod&space;{N}}}) for some linear polynomial 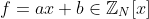 where b!=0. These two messages are to be sent by encrypting using the public key (N, e), thus giving ciphertexts C<sub>1</sub> and C<sub>2</sub> respectively. Then, given (N, e, C<sub>1</sub>, C<sub>2</sub>, f), the attacker can recover messages M<sub>1</sub> and M<sub>2</sub>.
10
+
Suppose there are two messages M<sub>1</sub> and M<sub>2</sub> where M<sub>1</sub> != M<sub>2</sub>, both less than N and related to each other as  for some linear polynomial  where b!=0. These two messages are to be sent by encrypting using the public key (N, e), thus giving ciphertexts C<sub>1</sub> and C<sub>2</sub> respectively. Then, given (N, e, C<sub>1</sub>, C<sub>2</sub>, f), the attacker can recover messages M<sub>1</sub> and M<sub>2</sub>.
So clearly M<sub>2</sub> is a root of both the polynomials above and hence they have a common factor **x-M<sub>2</sub>** (Since, g<sub>1</sub>(M<sub>2</sub>) = 0 and g<sub>2</sub>(M<sub>2</sub>) = 0)
23
23
Therefore, we can simply calculate GCD of g<sub>1</sub> and g<sub>2</sub> and if the resultant polynomial is linear, then we get out M<sub>2</sub> and hence M<sub>1</sub>!
0 commit comments