Math Library
Finds the absolute value of a complex number.
Finds the arccosine of a complex number.
Finds the hyperbolic arccosine of a complex number.
Adds two complex numbers.
Finds the phase angle of a complex number.
Finds the arcsine of a complex number.
Finds the hyperbolic arcsine of a complex number.
Finds the arctangent of a complex number.
Finds the hyperbolic arctangent of a complex number.
Finds the conjugate of a complex number.
Finds the cosine of a complex number.
Finds the hyperbolic cosine of a complex number.
Finds the cotangent of a complex number.
Finds the hyperbolic cotangent of a complex number.
Finds the cosecant of a complex number.
Finds the hyperbolic cosecant of a complex number.
Divides two complex numbers.
Finds the exponent of a complex number.
Imaginary part of a complex number.
Finds the inverse of a complex number.
Finds the logarithm of a complex number.
Finds the logarithm (base-10) of a complex number.
Finds the logarithm (base-B) of a complex number.
Copies a complex number into another.
Multiplies two complex numbers.
Finds the complex number for a given polar form.
Finds the power function of a complex number.
Real part of a complex number.
Finds the secant of a complex number.
Finds the hyperbolic secant of a complex number.
Finds the sine of a complex number.
Finds the hyperbolic sine of a complex number.
Finds the square root of a complex number.
Subtracts two complex numbers.
Finds the tangent of a complex number.
Finds the hyperbolic tangent of a complex number.
Calculates wet bulb temperature.
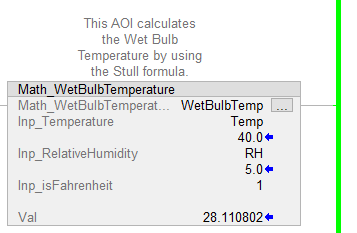
Background: Wet bulb temperature is used in cooling tower controls to give an indication of what temperature the cooling tower can achieve. If the wet bulb temperature is 14 degrees C, regardless of how hard you run the cooling tower, you won't be able to go past it (or even reach it). This gives you a limit that you can use as a floor for the cooling tower fan's PID setting to reduce the energy consumption at the fan.
Credit: cardosocea
- UDT: ST_Math_Complex
- UDT: ST_Math_Vector3D