【提问】用割平面法解整数规划问题时增加有效不等式的方法 #51
Description
1.是否已经阅读过所在章节的FAQ？
是
3.问题在教材中出处(章节，页码，截图)?
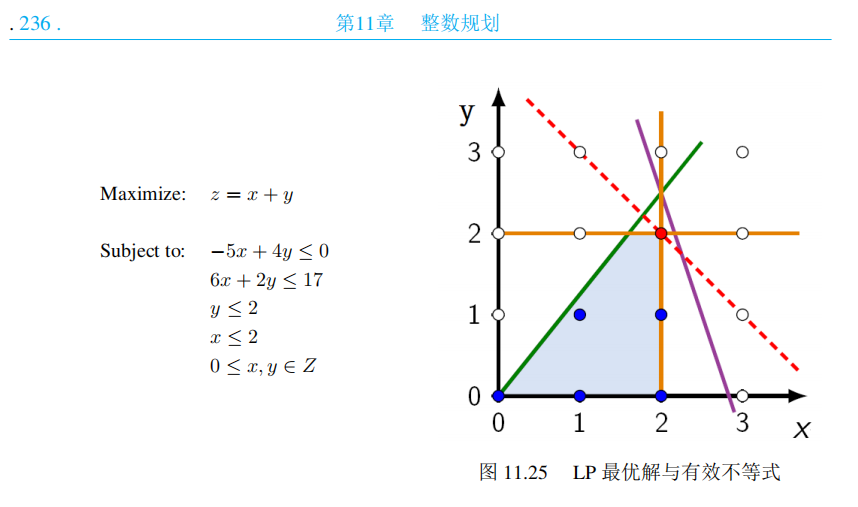
教材235-236页 例11.11
4.从网络搜索得到三篇参考资料并自学，请在下方附上网址。
https://wiki.mbalib.com/wiki/%E5%89%B2%E5%B9%B3%E9%9D%A2%E6%B3%95
https://zhuanlan.zhihu.com/p/28387290
5.综合学习教材、PPT、网络资源后仍然抱有疑问的原因？
Question
第1次进行割平面的操作中，书上使用的y<=2这个不等式；在第2次进行割平面的操作中，书上使用了x<=2这个不等式。都同样地让我困惑（除了用肉眼观察）。
假设原问题是这样：
那我们肯定不能之间把x或者y取整去作为它的割平面的操作（？）
Possible Solution 1
如果按我的想法，我觉得第1步也可以是：
当前x+y<=目前最优那个z的值 and x, y are intergers => x+y<=目前最优那个z的值向下取整=4
从而得到新的有效不等式 x+y<=4
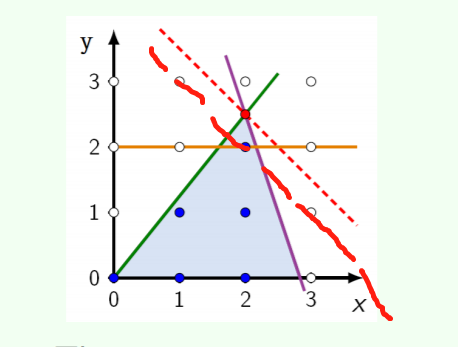
然后那条线段上就存在对应LP问题的无数个最优解，在里面找整数解。
但这个方法在x, y系数不是整数的时候就不行，或者如果靠近最优解的地方，那个凸包形成的万一是一个非常锐角的LP问题可行域，那把它只向下取整1个的时候，取整的位置也不会有最优解。
Possible Solution 2
要么使用某种随机的方法？在限定的一个区域内随机一个新的割平面，看看它是不是有效的割平面（保留了所有有效的整数解），如果不可以就重新取一个再进行判断。然后再通过某种方式证明它的极限是那个整数解。这样从计算机的角度可以在他收敛的时候就结束。
周子彦